Linear Equation in One Variable
The following are examples of statements of equality of two algebraic expressions
- 4(x-3) = 4x-12
- x^2 +3/x = (x^3+3)/x
- x+2 = 10
- x^2-3x = 18
- x+5 = x-7
- x^2-4x = x^2-4(x+3)
Statements 1 and 2 are true for all permissible values of 4. Such statements are called identities. Note that it is not permissible to assign the value 0 to x in statement 2.
Statements 3 and 4 are true for some but not all values of x. Statement 3 is true only if is 8. Statement 4 is true only if x is -3 or 6. Such statements are called equations.
Statements 5 and 6 are not true for any value of x and are called false statements.
DEFINITION The set of all numbers that satisfy an equation is called the solution set of the equation. The elements in the solution set are called the roots of the equation
To check whether a value of the variable is a root of the equation, substitute the value for the variable in the equation to see if the value of the right side of the equation is equal to the value of the left side of the equation.
DEFINITION An equation is said to be linear if the variables in the equation all have exponents of 1 and if no term of the equation has more than one variable as a factor.
The equation x+y-z = 1 is a linear equation in x,y, and z.
The equation x^2+x-6 is not a linear equation.
The equation 1x+xy = 9 is not a linear equation in x
This chapter deals with linear equations in one variable
Equivalent equations
DEFINITION Two equations are said to be equivalent if they have the same solution set.
The equations 5x + 7 = 2 and x = -1 are equivalent. The two equations have the same solution set, {-1}.
The solution sets of some equations are obvious by inspection. The solution set of the equation x + 4= 10 is {6}
To solve an equation, that is, to find its solution set, two theorems can be applied to get an equivalent equation whose solution is obvious.
THEOREM 1
Theorem 1 states that, given an equation P = Q, we can add any polynomial T in the same variable as P and Q to both sides of the equation, thus obtaining an equivalent equation P + T = Q + T.
The two equations 4x -1 = 3x +5 and 4x - 1 + (1 - 3x) = 3x + 5 + (1- 3x), which simplifies to x = 6, are equivalent. Their solution set is {6}.
THEOREM 2 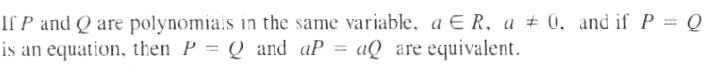
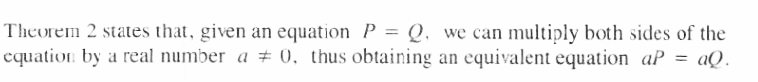
The two equations x = 2 and 5(x) = 5(2), that is, 5x = 10, are equivalent. Their solution set is {2}.
When both sides of an equation are multiplied by a constant different from zero, the resulting equation is equivalent to the original equation. However, when both sides of an equation are multiplied by an expression involving the variable, the resulting equation may not be equivalent to the original equation.
The two equations 2x = 8 and x(2x) = x(8), that is, 2x^2 = 8x, are not equivalent. The solution set of the equation 2x = 8 is {4}, while the solution set of the equation 2x^2 = 8x is {0,4}.
The two equationsx=3 and x(x+2) = 3(x+2) are not equivalent. The solution set of x=3 is{3}, while the solution set of x(x+2)=3(x+2) is {-2,3}.
Similarly, if we raise both sides of an equation
The two equations x = 5 and (x)^2 = (5)^2, that is, x^2 = 25, are not equivalent. The solution set of x = 5 is {5}, while the solution set of x^2 = 25 is {-5,5}.
Note The solution set of a linear equation in one variable has exactly one element.
Solving Equations
Given a linear equation in one variable, we may use one or both of the previous two theorems to form an equivalent equation of the form 1x = a, whose solution set is {a}.
When the coefficient of the variable in the equation is not 1, as in b/cx = d, an equivalent equation of the form 1x = a
The multiplicative inverse of b/c is c/b, since b/c*c/b = 1.
Thus when the coefficient of the variable is of the form b/c, multiply both sides of the equation by c/b.
EXAMPLE Find the solution set of the equation 14x = -21.
Solution The coefficient of x is 14
The multiplicative inverse of 14 is 1/14.
Multiply both sides of the equation by 1/14.
1/14(14x) = 1/14(-21) 1*x = -(21/14) x=-(3/2)
The solution set is {-(3/2)}.
Let’s see how our Linear equation solver solves this and similar equations. Click on "Solve Similar" button to see more examples.
EXAMPLE Find the solution set of the equation x/-4 = 12.
Solution The term x/-4 = -(1/4)x.
The coefficient of x is -1/4.
The multiplicative inverse of -(1/4) is -(4/1).
Multiply both sides of the equation by -(4/1)
-(4/1)(x/-4) = -(4/1)(12)
1*x = -48
x = -48
The solution set is {-48}.
Note Since x stands for 1x, we omit the 1.
EXAMPLE Find the solution set of the equation 5/7x = 15
Solution
The multiplicative inverse of 5/7is 7/5.
Multiply both sides of the equation by 7/5.
7/5*5/7x = 7/5(15)
Hence x = 7/5*15/1 = 21
The solution set is {21}
EXAMPLE Find the solution set of the equation 1.3x = -39.
Solution When the coefficient of the variable is in decimal form, it will be easier if it is changed to a common fraction:
1.3x = -39 is equivalent to 13/10x = -39
Multiply both sides of the equation by 10/13
10/13*13/10x = 10/13(-39)
Hence x = 10/13 * -39/1 = -((10*39)/13) = -30
The solution set is {-30}
Let’s see how our Math calculator solves this and similar equations. Click on "Solve Similar" button to see more examples.
EXAMPLE Find the solution set of the equation -((7x)/8) = 35/36.
Solution The coefficient of x is -(7/8).
The multiplicative inverse of -(7/8) is -(8/7)
Multiply both sides of the equation by -(8/7)
-(8/7)(-(7/8)x) = -(8/7)(35/36)
Hence x = -((8*35)/(7*36)) = -(10/9)
The solution set is {10/9}.
When the equation has more than one term containing the variable as a factor, combine the terms, utilizing the distributive law of multiplication.
EXAMPLE Find the solution set of the equation 3x+4x-2x = 8.
Solution
3x+4x-2x = 8
(3+4+2)x = 8
5x = 8
Hence x = 8/5
The solution set is {8/5}.
When some of the terms of an equation contain fractions, to facilitate combining like terms, form an equivalent equation containing only integers. To accomplish this. multiply both sides of the equation by the, least common multiple of the denominators of the fractions.
Remember, multiplying both sides of an equation by a number different from zero results in an equivalent equation.
Note The least common multiple can be obtained as follows;
1. Factor the integers into their prime factors and write the factors in the exponent form.
2. Take all the buses, each to its highest exponent.
EXAMPLE Find the LCM of 12,16,18.
Solution 12 = 2*2*3 = 2^2*3
16 = 2*2*2*2 = 2^4
18 = 2*3*3 = 2*3^2
The bases are 2 and 3. The highest exponent of 2 is 4 and that of 3 is 2.
Hence the LCM = 2^4 * 3^2 = 16*9 = 144
EXAMPLE Find the solution set of the equation 3/4x-1/3x = 5
Solution We first find the LCM of 4 and 3.
4 = 2^2, 3 = 3
LCM = 2^2 * 3 = 12
Multiply both sides of the equation by 12/1:
12/1(3/4x-1/3x) = 12/1(5)
12/1(3/4x) + 12/1(-(1/3)x) = 60
9x-4x = 60
x = 12
The solution set is {12}.
EXAMPLE Find the solution set of the equation
8/9x - 1/6x - 3/4x = 1/8
Check the answer.
Solution First find the LCM of 9,6,4 and 8,
9 = 3^2, 6 = 2*3, 4=2^2, 8 = 2^3
LCM = 2^3*3^2 = 72
Multiply both sides of the equation by 72/1:
72/1(8/9x-1/6x-3/4x) = 72/1(1/8)
72/1(8/9x)+72/1(-(1/6)x)+72/1(-(3/4)x) = 9
64x-12x-54x = 9
(64-12-54)x = 9
-2x = 9
x = -9/2
To check the answer, substitute -9/2 for x in each side of the original equation separately:
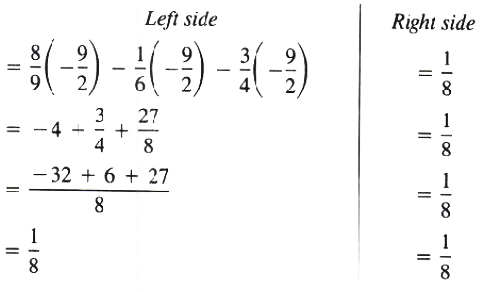
The solution set is {-9/2}.
Let’s see how our Linear equation solver solves this and similar equations. Click on "Solve Similar" button to see more examples.
EXAMPLE List the elements in the set ![]()
Solution Consider the statement
2x + 3x - 5x = 0
(2 + 3 - 5)x = 0
0x = 0
Since 0x = 0 is true for any real value of x, we have
![]()
EXAMPLE List the elements in the set
![]()
Solution Consider the statement
10x-8x-2x = 4
(10-8-2)x = 4
0x = 4
Since 0x = 4 is not true for any real value of x, we have
![]()
Sometimes both sides of the equation contain terms that have the variable as a factor and also terms that do not have the variable as a factor. To find the solution set of the equation, form an equivalent equation that has all terms with the variable as a factor on one side of the equation. The terms not having the variable as a factor must appear on the other side.
The equivalent equation can be formed by adding the negative (additive inverse) of the terms to both sides of the equation.
Consider the equation 8x-5 = 6x+7
Add (+5) to both sides: 8x-5+5 = 6x+7+5
8x+0 = 6x+12
8x = 6x +12
Add (-6x) to both sides: 8x+(-6x) = 6x+12+(-6x)
2x = 12
x = 6
The solution set is {6}.
Remark It is important to realize the difference between the two equations
3x = 15 and 3+x = 15
In 3x = 15, the 3 is the coefficient of x; thus to solve for x, multiply both sides of the equation by (1/3).
1/3(3x) - 1/3(15)
x = 5
The solution set is {5}.
In 3+x = 15, the 3 is a term; thus to solve for x, add (-3) to both sides of the equation.
3+x+(-3) = 15+(-3)
x = 12
The solution set is {12}.
EXAMPLE Solve the equation 2x-x-3 = 10+7x-4
Solution Add (+3 -7x) to both sides of equation.
2x-x-3+(+3-7x)-10+7x-4+(+3-7x)
2x-x-3+3-7x = 10+7x-4+3-7x
-6x = 9
x = -(9/6) = -(3/2)
The solution set is {-3/2}.
Note When the equation contains mixed numbers, change the mixed numbers to improper fractions.
EXAMPLE Solve the equation 31/2x-22/3x-7 = x/6+12/3.
Solution First change the mixed numbers to improper fractions
7/2x-8/3x-7 = x/6+5/3
Multiply both sides of the equation by the least common multiple of 2, 3, 6, and 3, which is 6.
6/1(7/2x-8/3x-7) = 6/1(x/6+5/3)
6/1(7/2x)+6/1(-8/3x)+6/1(-7) = 6/1(x/6)+6/1(5/3)
21x-16x-42 = x+10
Add (+42-x) to both sides of equation.
21x-16x-42+42-x = x+10+42-x
4x = 52
x = 13
The solution set is {13}.
Let’s see how our Linear equation calculator solves this and similar equations. Click on "Solve Similar" button to see more examples.