Linear relations and their graphing
LINEAR RELATIONS
In this section we examine one of the simplest types of relations, the linear relation. Every linear relation has a graph that is a straight line, and so we need only find two points on the graph in order to sketch it. Examples of linear relations arey=2x+3 , y=x and 3x + 2y = 6
LINEAR RELATION A linear relation in two variables is a relation that can be written in the form
y=ax+b,
where a and b are real numbers.
Note Linear relations are often written in the form Ax + By = C , where A, B, and C are real, and A and B are not both 0. This is called the standard form of a linear relation.
In the equation Ax + By = C, any number can be used for x or y, so both the domain and range of a linear relation in which neither Anor B is 0are the set of real numbers (-inf,inf),
GRAPHING LINEAR RELATIONS. The graph of a linear relation can be found by plotting at least two points. Two points that are especially useful for sketching the graph of a line are found with the intercepts. An x-intercept is an x-value at which a graph crosses the x-axis. A y-intercept is a y-value at which a graph crosses the y-axis. Since y = 0 on the x-axis, an x-intercept is found by setting y equal to 0 in the equation and solving for x. Similarly, a y-intercept is found by settingx=0 in the equation and solving for y.
Example 1 GRAPHING A LINEAR RELATION USING INTERCEPTS
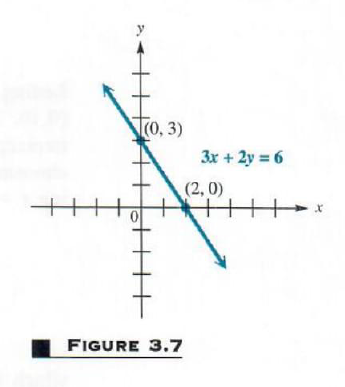
Graph 3x + 2y = 6.
Use the intercepts. The y-intercept is
found by lettingx=0.
3.0+2y=6
2y=6
y=3
For the x-intercept, let y=0, getting
3x+2.0=6
3x=6
x=2.
Plotting (0,3) and (2,0) gives the graph in Figure 3.7. A third point could be found as a check if desired.
Let’s see how our math solver generates graphs of this and similar problems. Click on "Solve Similar" button to see more examples.
Example 2 GRAPHING HORIZONTAL AND VERTICAL LINES
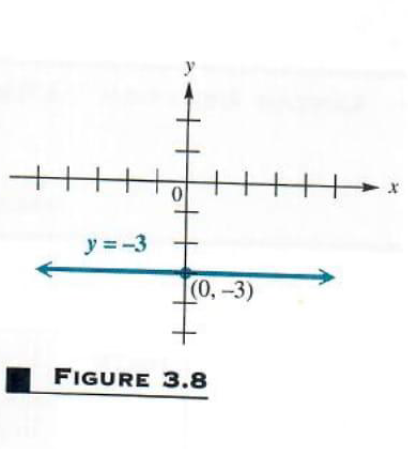
(a) Graph y=-3.
Since y always equals -3, the value of y can never be 0. This means that the graph has no x-intercept. The only way a straight line can have no x-intercept is for it to be parallel to the x-axis, as shown in Figure 3.8. Notice that the domain of this linear relation is (-inf,inf) but the range is {-3}.
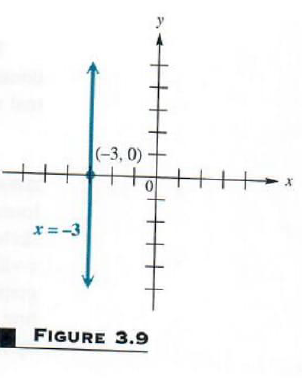
(b) Graph x=-3.
Here, since x always equals -3, the value of x can never be 0, and the graph has no y-intercept. Using reasoning similar to that of part (a), we find that this graph is parallel to the y-axis, as shown in Figure 3.9. The domain of this relation is {-3}, while the range is (-inf,inf),
From this example we may conclude that a linear relation of the form y=k has as its graph a horizontal line through (0,k), and one of the form x=k has as its graph a vertical line through (k,0).
Example 3 GRAPHING A LINE THROUGH THE ORIGIN
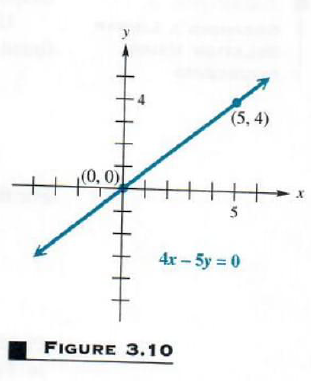
Graph 4x-5y=0,
Find the intercepts. If x=0, then
4(0)-5y=0
-5y=0 y=0
Letting y=0 leads to the same ordered pair,0=0. The graph of this relation has just one intercept—at the origin. Find another point by choosing a different value for x (or y). Choosing x=5 gives
4(5)-5y=0
20-5y=0
20=5y
4=y
which leads to the ordered pair (5,4). Complete the graph using the two points (0,0) and (5,4), with a third point as a check. See Figure 3.10.
Let’s see various graphs of line passing through origin. Click on "Solve Similar" button to see more examples.
SLOPE An important characteristic of a straight line is its slope, a numerical measure of the steepness of the line. (Geometrically, this may be interpreted as the ratio of rise to run.) To find this measure, start with the line through the two distinct points (x_1,y_1) and (x_2,y_2), as shown in Figure 3.11 , where (x_1!=x_2).The difference
(x_2-y_1)
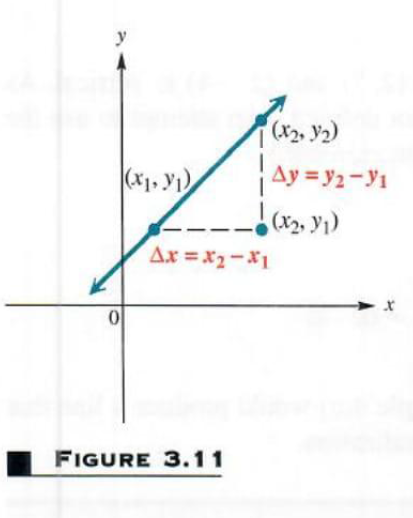
is called the change in x and denoted by {Delta}(x) (read “delta x’), where {Delta} is the Greek letter delta. In the same way, the change in y can be written
{Delta}y=y_2-y_1
The slope of a nonvertical line is defined as the quotient of the change in y and the change in x, as follows.
SLOPE The slope m of the line through the points (x_1,y_1) and (x_2,y_2) is
m=({Delta}y)/({Delta}x)=(y_2-y_1)/(x_2-x_1)
Where {Delta}(x)!=0
CAUTION When using the slope formula, be sure that it is applied correctly. It makes no difference which point is (x_1,y_1) or (x_2,y_2); however, it is important to be consistent. Start with the x- and y-value of one point (either one) and subtract the corresponding values of the other point.
The slope of a line can be found only if the line is nonvertical. This guarantees that (x_2!=x_1), so that the denominator (x_2-x_1)!=0. It is not possible to define the slope of a vertical line.
The slope of a vertical line is undefined.
Example 4.FINDING SLOPES WITH THE SLOPE FORMULA
Find the slope of the line through each of the following pairs of points.
(a) (-4, 8), (2, -3)
Let x_1=-4, y_1=8, and x_2=-2, y_2=-3. Then
{Delta}y=-3-8=-11
and x{Delta}=2-(-4)=6
The Slope is m=({Delta}y)/({Delta}x)=-11/6
(b) (2, 7), (2, -4)
A sketch would show that the line through (2, 7) and (2, -4) is vertical. As mentioned above, the slope of a vertical line is not defined. (An attempt to use the
definition of slope here would produce a zero denominator.)
(c) (5, -3) and (-2, -3)
By definition of slope,
m=(-3-(-3))/(-2-5)=0/-7=0
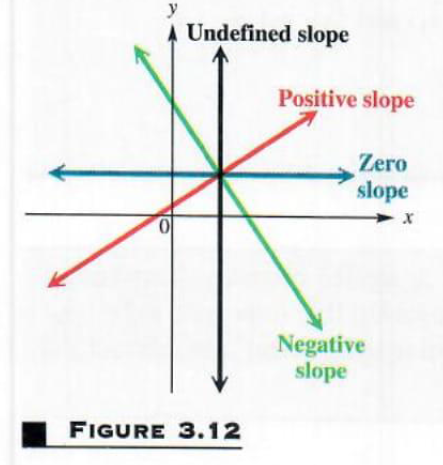
Drawing a graph through the points in Example 4(c) would produce a line that is horizontal, which suggests the following generalization.
The slope of a horizontal line is 0.
Figure 3.12 shows lines of various slopes. As the figure shows, a line with a positive slope goes up from left to right, but a line with a Positive slope negative slope goes down from left to right.
It can be shown, using theorems for similar triangles, that the slope slope is independent of the choice of points on the line. That is, the slope of a line is the same no matter which pair of distinct points on the line are used to find it.
Since the slope of a line is the ratio of vertical change to horizontal change, if we know the slope of a line and the coordinates of a point on the line, the graph of the line can be drawn. The next example illustrates this.
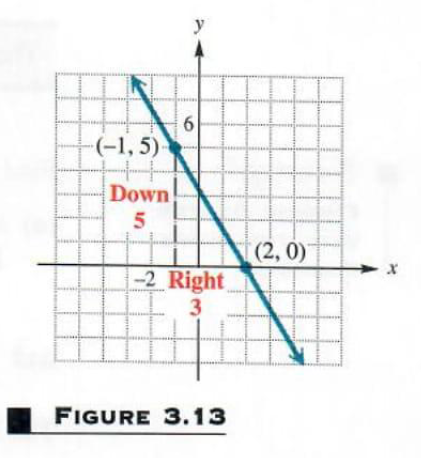
Example 5 GRAPHING A LINE USING A POINT AND THE SLOPE
Graph the line passing through (-1,5) and having slope-5/3.
First locate the point (-1,5) as shown in Figure 3.13. Since the slope of this line is -5/3, a change of -5 units vertically (that is, 5 units down) produces a change of 3 units horizontally (3 units to the right).
This gives a second point, (2,0), which can then be used to complete the graph.
Because -5/3=5/(-3), another point could be obtained by starting at (-1,5)and moving 5 units up and 3 units to the left. We would reach a different second point, but the line would be the same.
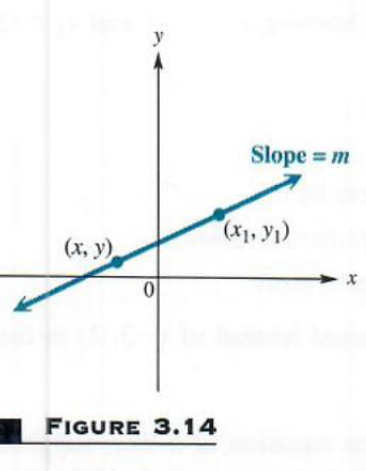
EQUATIONS OF A LINE Since equations can define relations, we now consider methods of finding equations of linear relations. Figure 3.14 shows the line passing through the fixed point (x_1,y_1) and having slope m. (Assuming that the
line has a slope guarantees that it is not vertical.) Let (x,y) be any other point on the line. By the definition of slope, the slope of the line is
(y-y_1)/(x-x_1)
Since the slope of the line is m,
(y-y_1)/(x-x_1)=m
Multiplying both sides by x-x_1 gives
y-y_1=m(x-x_1)
This result, called the point-slope form of the equation of a line, identifies points on a given line: a point (x,y) lies on the line through (x_1,y_1) with slope m if and only if
y-y_1=m(x-x_1)
POINT-SLOPE FORM The line with slope m passing through the point (x_1,y_1) has an equation
y-y_1=m(x-x_1)
the point-slope form of the equation of a line.
Example 6 USING THE POINT-SLOPE FORM (GIVEN A POINT AND THE SLOPE)
Write an equation of the line through (-4,1) with slope -3.
Here x_1=-4, y_1=1, and m=-3. Use the point-slope form of the equation of a line to get
y-1=-3[x-(-4) x_1=-4 y_1=1 m=-3
y-1=-3(x+4)
y-1=-3x-12) Distributive property
or 3x+y=-11
in standard form.
CAUTION The definition of “standard form” is not standard from one text to another. Any linear equation can be written in many different (all equally correct) forms. For example, the equation 2x+3y=8 can be written as 2x=8-3y , 3y=8-2x ,x+3/2y=4,4x+6y=16 and so on. In addition to writing it in the form Ax + By = C (with A>=0), let us agree that the form 2x+3y=8 is preferred over any multiples of both sides, such as 4x+6y=16.
Example 7 USING THE POINT-SLOPE FORM (GIVEN TWO POINTS)
Find an equation of the line through (-3,2) and (2,-4)
Find the slope first. By the definition of slope,
m=(-4-2)/(2-(-3))=-6/5
Either (-3,2) or (2,-4) can be used for (x_1,y_1). Choosing (x_1=-3 and (y_1=2 in the point-slope form gives
y-2=-6/5[x-(-3)
5(y-2)=-6(x+3) Multiply by 5.
5y-10=-6x-18 Distributive property
(6x+5y=-8 Standard form
Verify that the same equation results if (2,-4) is used instead of (-3,2) in the Point-slope form.
As a special case of the point-slope form of the equation of a line, suppose that a line passes through the point (0, b), so the line has y-intercept b. If the line has slope m, then using the point-slope form with x_1=0 and y_1=b gives
y-y_1=m(x-x_1)
y-b=m(x-0)
y=mx+b
as an equation of the line. Since this result Shows the slope of the line and the y-intercept, it is called the slope-intercept form of the equation of the line.
SLOPE-INTERCEPT FORM The line with slope m and y-intercept b has an equation
y=mx+b
the slope-intercept form of the equation of a line.
Example 8 USING THE SLOPE-INTERCEPT FORM TO GRAPH A LINE
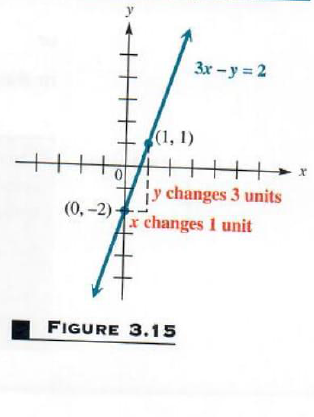
Find the slope and y-intercept of 3x-y=2 Graph the line using this information.
First write 3x-y=2 in the slope-intercept form, y=mx+b, by solving for y, getting 3x-y=2. This result shows that the Slope is m=3 and the y-intercept is b=-2. To draw the graph, first locate the y-intercept. See Figure 3.15. Then, as in Example 5, use the slope of 3, or 3/1, to get a second point on the graph. The line through these two points is the graph of 3x-y=2.
In the preceding discussion, it was assumed that the given line had a slope. The only lines having undefined slope are vertical lines. The vertical line through the point (a, b) passes through all the points of the form (a, y) , for any value of y. This fact determines the equation of a vertical line.
EQUATION OF A VERTICAL LINE An equation of the vertical line through the point (a, b) is x=a
For example, the vertical line through (-4,9) has equation x=-4, while the vertical line through (0,1/4) has equation x=0. (This is the y-axis.)
The horizontal line through the point (a, b) passes through all points of the
form (x, b) , for any value of x. Therefore, the equation of a horizontal line involves only the variable y.
EQUATION OF A HORIZONTAL LINE An equation of the horizontal line through the point (a, b) is y=b.
For example, the horizontal line through (1,-3) has the equation y=-3. See Figure 3.8 for the graph of this equation. The equation of the x-axis is y=0.
PARALLEL. AND PERPENDICULAR LINES Slopes can be used to decide whether or not two lines are parallel. Since two parallel lines are equally “steep,” they should have the same slope. Also, two distinct lines with the same “steepness” are parallel. The following result summarizes this discussion.
PARALLEL LINES Two distinct non vertical lines are parallel if and only if they have the same slope.
Slopes are also used to determine if two lines are perpendicular. Whenever two lines have slopes with a product of -1, the lines are perpendicular.
PERPENDICULAR LINES Two lines, neither of which is vertical, are perpendicular if and only if their slopes have a product of -1.
For example, if the slope of a line is -3/4, the slope of any line perpendicular
to it is 4/3, since (-3/4)(4/3)=-1. We often refer to numbers like -3/4 and 4/3 as “negative reciprocals.” A proof of this result is outlined in Exercises 63-66.
Example 9
USING THE SLOPE RELATIONSHIPS FOR PARALLEL AND PERPENDICULAR
Find the equation of the line that passes through the point (3,5) and satisfies the given condition.
(a) parallel to the line 2x+5y=4
Since it is given that the point (3,5) is on the line, we need only find the slope to use the point-slope form. Find the slope by writing the equation of the given line in slope-intercept form. (That is, solve for y.)
2x+5y=4
y=-2/5x+4/5
The slope is -2/5. Since the lines are parallel, -2/5 is also the slope of the line whose equation is to be found. Substituting m=-2/5, x_1=3, and y_1=5 into the point-slope form gives
y-y_1=m(x-x_1)
y-5=-2/5(x-3)
5(y-5)=-2(x-3)
5y-25)=-2x+6
2x+5y=31
(b) perpendicular to the line 2x+5y=4
In part (a) it was found that the slope of this line is -2/5, so the slope of any line perpendicular to it is 5/2. Therefore, use m=5/2, x_1=3, and y_1=5 in the point-slope form.
y-5=5/2(x-3)
2(y-5)=5(x-30
2y-10=5x-15
-5x+2y=-5
or 5x-2y=5
All the lines discussed above have equations that could be written in the form
Ax + By = C for real numbers A, B, and C. As mentioned earlier, the equation Ax + By = C is the standard form of the equation of a line. The various forms of linear equations are listed below.
LINER EQUATIONS
| General Equation | Type of Equation |
| Ax+by=C | Standard form (if A!=0 and B!=0),x-intercept C/A, y-intercept C/B, slope -A/B |
| x=k | Vertical line x-intercept k, no y -intercept, undefined slope |
| y=k | Horizontal line y-intercept k, no x-intercept, slope 0 |
| y=mx+b | Slope-intercept form, y-intercept b, slope m |
| y-y_1=m(x-x_1) | Point-slope form , slope m, through (x_1,y_1) |
PROBLEM SOLVING
A straight line is often the best approximation of a set of data points that result from a real situation. If the equation is known, it can be used to predict the value of one variable, given a value of the other. For this reason, the equation is written as a linear relation in slope-intercept form. One way to find the equation of such a straight line is to use two typical data points and the point-slope form of the equation of a line.
Example 10 FINDING AN EQUATION FROM DATA POINTS
Scientists have found that the number of chirps made by a cricket of a particular Species per minute is almost linearly related to the temperature. Suppose that for a particular species, at 68°F a cricket chirps 124 times per minute, while at 80° F the cricket chirps 172 times per minute. Find the linear equation that relates the number of chirps to the temperature.
Think of the ordered pairs in the relation as (chirps, temperature), or (c, t). Then c takes on the role of x and t takes on the role of y. Since we are using a linear relationship, find the slope of the line by using the slope formula with the points (124,68) and (172,80).
m=(68-80)/(124-172)=-12/-48=1/4
Choose one of the points, say (124,68), and substitute into the point-slope form, with m=1/4.
t-68=1/4(c-124)
t-68=1/4c-31
t=1/4c+37
The equation is t=1/4c+37. By substituting the number of chirps per minute into this equation, the temperature t can be approximated.