Number System
1.1 The Natural Numbers and Whole Numbers
By the natural numbers we mean the collection or set of numbers 1, 2, 3, 4,... , which are the numbers that we use for counting. This set is denoted by the symbol N and we use the notation
N={1,2,3,4,...}
the three dots denoting that the process continues. By the set of whole numbers we mean the set that includes the natural numbers and also zero. This set is denoted by W. Thus
W={0,1,2,3,4,...}
We may visualize the whole numbers by establishing a correspondence between these numbers and certain points on a ray or half line as follows: Choose two points O and A, with A to the right of O. With O as the starting point, draw the half line from O through A. Using the distance from O to A as the unit distance, we now mark off successive points, one unit apart, on the half line as shown in Figure 1. We now

FIGURE 1.
let the number 0 correspond to the point O, we let 1 correspond to A, 2 correspond to B, and so on, as shown in Figure 2. ln this correspondence a number is the coordinate of its corresponding point.

FIGURE 2.
We are familiar with the operations of addition and multiplication of whole numbers. The property that the sum of two whole numbers is again a whole number is called the closure law for addition. Similarly, since the product of two whole numbers is again a whole number, the closure law of multiplication holds for W . The basic laws for computations in W are the following: for m, n, and p whole numbers,
A.1 m + (n + p) = (m + n) + p (associative law of addition)
A.2 m + n = n + m (commutative law of addition)
A.3 n+ 0 = n (additive identity)
M.1 m * (n * p) = (m * n) *p (associative law of multiplication)
M.2 m*n=n*m (commutative law of multiplication)
M.3 1*n=n (multiplicative identity)
D.1 n * (m+ p) = (n * m) + (n * p) (left distributive law)
D.2 (m+ p) * n = (m * n) + (p * n) (right distributive law)
Two other operations on W are subtraction and division. Subtraction is defined in terms of addition in the following way. If m and n are whole numbers, then m-n is the whole number x such that
n+x=m
if such a whole number x exists. Division is defined in terms of multiplication. If m and n are whole numbers and n!=0, then m ÷ n is the whole number x such that
n*x=m
if such a whole number x exists.
Notice that division by 0 is not defined. For if m!=0, then there is no whole number x such that 0*x=m; and if m = 0, then every whole number x satisfies 0*x=0. We also notice that subtraction is not a closed operation on W. For example, 1-2 is not a whole number. Division is not closed either, since, for example, 3÷4 is not a whole number. As we know, in order to make subtraction a closed operation we must extend the whole numbers to the integers, and to make division a closed operation we must extend the integers to the rational numbers. These number systems will be considered in sections 1.2 and 1.3.
The natural numbers have some interesting multiplicative properties that we will now consider. If a,b, and c are natural numbers and c = a * b, then a and b are said to be factors or divisors of c, and c is said to be a multiple of a and of b. We note that 1 is a factor of every natural number c since c = 1 * c. We refer to 1 as a trivial factor of c, and c as a trivial multiple of itself. A natural number c other than 1 is a prime if the only divisors of c are 1 and c. For example 3 is a prime since its only factors are 1 and 3, while 4 is not prime since 4 = 2 * 2. A natural number is called even if it has a factor of 2 and it is called odd if it is not even. The numbers 2, 4, 6, ..., are all even while 1, 3, 5, ... , are odd. It follows that a natural number a is even if and only if a = 2b, where b is a natural number, and ais odd if and only if a = 2b-1, where b is a natural number.
By trial it is easy to see that the first six primes are 2, 3, 5, 7, 11, and 13. Since every nontrivial multiple of a given natural number is non-prime, the following process, due to the Greek mathematician Eratosthenes (275-194 B.C.), can be used to find all of the primes less than a given natural number.
Example 1. Find all of the primes less than 50.
First write all the natural numbers from 1 to 50 in succession.
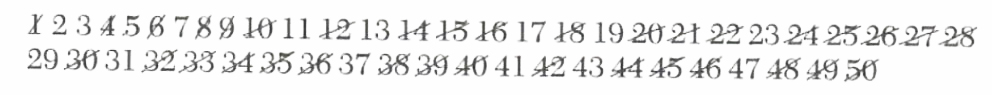
Since 1 is not a prime we cross it out. Since 2 is prime and every nontrivial multiple of 2 is not prime, we keep 2 and cross out every second number thereafter. Then keep the next uncrossed number, that is, 3, and cross out every third number thereafter. Then keep the next uncrossed number, that is, 5, and cross out every fifth number thereafter. Continuing this process, the numbers left uncrossed at the end are primes.
The number of primes is known to he infinite; in fact, the famous Greek mathematician Euclid (circa 300 B.C.) published a proof that there is no greatest prime.
Every natural number greater than 1 can be expressed as a product of prime factors in one and only one way, apart from the order in which the factors are written. This result is known as the Unique Factorization Theorem. For example, the unique factorization of 56, 60, 90, and 113 are:
56=2*2*2*7
60=2*2*2*5
90=2*3*3*5
113=113
The problem of finding the prime factors of a given natural number is a diflicult one. If you are unconvinced, try to factor your social security number into primes. We will find the following rules helpful:
F.1 If the last digit ofa natural number is even, then it has a factor of 2.
F.2 If the last digit of a natural number is 0 or 5, then it has a factor
of 5.
F.3 If the sum of the digits o fa natural number is divisible by 3, then
it has 3 as a factor.
For example, 192, 768, and 24 have 2 as a factor, 250, 145, and 760 have 5 as a factor, while 123, 504, and 273 all have 3 as a factor. These may all be verified by the reader.
F.4 When we are trying to find factors of a natural number a, if b*b is greater than a, then a has no factors greater than b if it has none less than b.
Rule F.4 is useful in determining whether or not a number is a prime. For example, in determining whether 113 is prime, the only numbers that we need try are the primes less than 11 since 11 * 11 = 121, which is bigger than 113.
In computing the prime factorization of 258 we first find the 2’s that are factors by successive division by 2, then the 3's that are factors, and so on. Rules F.1 through F.4 will help us in the computation, especially F.4 which allows us to reduce the number of primes that we must try as divisors.
Example 1. Write 258 as a product of primes.
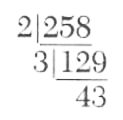
We see that 43 is not divisible by 2, 3, 5, or 7. From rule F.4, since - 7*7= 49, there are no larger divisors and thus 43 is prime. Consequently
258=2*3*43
Example 2. Write 113 as a product of primes
First we see that 113 is not divisible by 2, 3, 5, 7, or 11, where 11* 11 = 121. By rule F.4 it follows that 113 is prime. Thus
113= 113
If a_1,a_2,...,a_n, are natural numbers, then the least common multiple of a_1,a_2,...,a_n, is the smallest natural number that is a multiple of each a_i. We denote this number by L.C.M. (a_1,a_2,...,a_n). In order to compute the L.C.M. of a finite collection of natural numbers we form the product of the primes obtained by taking each prime factor that occurs in any of the numbers the maximum number of times it occurs in any of the numbers.
Example 3. Find L.C.M. (6,8,12).
Since 6=2*3
8=2*2*2
12=2*2*3
L.C.M.(6,8,12)=2*2*2*3
=24
Example 4. Find L.C.M.(40,48,56,24).
Since 40=2*2*2*5
48=2*2*2*2*3
56=2*2*2*7
and 24=2*2*2*3
L.C.M.(40,48,56,24)=2*2*2*2*3*5*7
1.2 The Integers
In Section 1.1 we saw that some differences, m-n, are not whole numbers. In order to obtain a collection of numbers in which subtraction is closed, we first extend our number line to the left of zero and mark off points one unit apart starting with the point whose coordinate is 0. Then, to distinguish the coordinates of the points on the left from those on the right we attach negative signs to the ones on the left. See Figure 3. The resulting collection of numbers, denoted by Z,
![]()
FIGURE 3.
is called the integers. Thus
Z={...,-3,-2,-1,0,1,2,3,4...}
The coordinate of each point to the right of zero is called (as well as a natural number) a positive integer, and the coordinate of each point to the left of zero is called a negative integer. Zero is neither positive nor negative. Thus Z is made up of the positive integers, the negative integers, and zero.
The set of integers is closed under the operations of addition, multiplication, and also subtraction. However, Z is not closed under division, since 3+4 is not an integer. The system Z satisfies all of the laws that W satisfies, that is, A.1 through D.2, along with:
A.4 For each integer m there is a unique integer, denoted by -m, such that
m+(-m)=0 (additive inverse)
The integer -m is called the additive inverse of m, or the negative of m. Notice that -m is a negative number if m is positive, but -m is a positive number if m is negative. For example if m = -3, its additive inverse, -m, is -(-3). However,
-3+3=3+(-3)=0
thus 3 is the additive inverse of -3, consequently,
-(-3)=3
The following important rules of computation in Z follow from the basic rules A.1 through D.2, including A.4. For m and n integers,
C.1 -(-m)=m
C.2 m+(-n)=m-n
C.3 m-(-n)=m+n
C.4 0*m=0
C.5 (-1)m=-m
C.6 m(-n)=(-m)n=-(m*n)
C.7 (-m)(-n)=m*n
C.8 -(m+n)=-m-n
C.9 -(m-n)=-m+n
The rule C.1 is derived as follows. Since
-m+m=m+(-m)=0
mis the additive inverse of -m. Thus
-(-m)=m
We are not emphasizing proofs; therefore, we leave the derivations of C.2 through C.9 to the interested reader.
Example 1. Compute each of the following (a) 7+(-3) (b) -4+(-9).
(a) 7+(-3)=7-3 (C.2)
=4
(b) -4+(-9)=-4-9 (C.2)
=-13
Example 2. Compute each of the following: (a) 4-(-2) (b) -12-(-10).
(a) 4-(-2)=4+2 (C.3)
=6
(b) -12-(-10)=-12+10 (C.3)
=-2
Example 3. Compute each of the following: (a) -(5-9) (b) (-1)[7+(-12)] (c) (-7)(-2) (d) 3(-5)
(a) -(5-9)=-(-4) (C.1)
=4
(b) (-1)[7+(-12)]=(-1)(-5)
=-(-5) (C.5)
=5 (C.1)
(c) (-7)(-2)=7*2 (C.7)
=14
(d) 3(-5)=-(3*5) (C.6)
=-15
In our last two examples we consider more complicated computations.
Example 4. Compute each of the following: (a) 2+(3-8) (b) -4-[7+(-3)] (c) (-8+12)-[-3-(-2)] (d) -2-{3+[-7-(3-2)]}
(a) 2+(3-8)=2+(-5)
=2-5=-3
(b) -4-[7+(-3)]=-4-[7-3]
=-4-[4]=-8
(c) (-8+12)-[-3-(-2)]=4-[-3+2]
=4-[-1]
=4+1=5
(d) -2-{3+[-7-(3-2)]}=-2-{3+[-7-1]}
=-2-{3+[-8]}
=-2-{-5}
=-2+5=3
Note that for these numerical computations we begin with the inner most set of parentheses.
Let’s see how our Number system solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
Example 5. Compute each of the following (a) (-5+9)(3-12) (b) 2-3(1-5) (c) [-6+7(4-5)]-2[-4+(6-1)] (d) -3-2[7-5(-2-3(1-5))]
(a) (-5+9)(3-12)=(4)(-9)
=-36
(b) 2-3(1-5)=2-3(-4)
=2-[-(3*4)]
=2+12=14
(c) [-6+7(4-5)]-2[-4+(6-1)]=[-6+7(-1)]-2[-4+5]
=[-6-7]-2[1]
=-13-2=-15
(d) -3-2[7-5(-2-3(1-5))]=-3-2{7-5[-2-3(-4)]}
=-3-2{7-5[-2+12]}
=-3-2{7-5[10]}
=-3-2{7-50}
=-3-2{-43}
=-3+86=83
Unique factorization holds in Z as well as in N. For example
-24=-(2*2*2*3)
Consequently, we also have the notion of least common multiple in Z. To find the least common multiple of a set of integers we ignore the signs and compute the L.C.M. of the resulting natural numbers.
Example 5. Compute L.C.M.(-12,14,-15).
Since 12=2*2*3
14=2*7
15=3*5
then L.C.M.(-12,14,-15)=2*2*3*5*7
=420
1.3 Rational Numbers
In order to obtain a collection of numbers that will be closed under division, we enlarge our system to the collection of rational numbers. This collection is
Q={a/b, where a and b are integers and b!=0}
The integer b has to be different from zero since division by zero is not defined. Note that the integers are rational numbers since the integer n is equal to the rational number n/1. The rational numbers can be assigned as coordinates of certain points on the number line. For example, 2/3 corresponds to the point obtained by dividing the segment from the point whose coordinate is 0 to the point whose coordinate is 1 into three equal segments and then taking the second

point of the subdivision. In the case of -(7/5), we write
-(7/5)=-1-2/5
and then divide the segment from -1 to -2 into five equal parts. The number -(7/5) corresponds to the second subdivision point counting from -1. From now on we will refer to the point whose coordinate is a, simply as the point a.

We know that the rational numbers 1/2, 2/4, 3/6, ..., all represent the same rational number. Therefore, for the first time we have encountered a system where equality is not to be taken for granted. In fact the law of equality for rational numbers is: If a/b and c/d are rational numbers, then
a/b=c/d if and only if ad=bc
For example,
2/4=1/2 since 2*2=4*1
and
-3/8=6/-16 since (-3)(-16)=8*6
This definition allows us tn derive the fundamental cancellation law for rational numbers. If a, b, and c are integers, b!=0, and c!=0, then
(a*c)/(b*c)=a/b
This follows easily since ac(b)=a(bc) because of associativity and commutativity of multiplication for integers. This is called the cancellation law because in practice we write
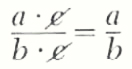
A rational number a/b is said to be in simplest form if a and b have no nontrivial factors in common, To simplify a/b we factor the integers a and b into prime factors and then use the cancellation law.
Example 1. Write 60/72 in simplest form.
Since 60=2*2*3*5
and 72=2*2*2*3*3
we have
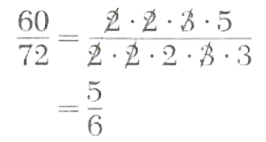
If a/b and c/d are rational numbers, then multiplication is defined by the equation
a/b*c/d=(a*c)/(b*d)
For example,
1/3*2/5=(1*2)/(3*5)
=2/15
(3/5)*(7/-6)=(3*7)/(5(-6))
=(3*7)/(-5*2*3)
=7/-10
The definition of division for rational numbers is the same as it is for natural numbers. If a/b and c/d are rational numbers and c!=0, then (a)/(b)÷c/d is the rational number x/y such that
c/d*x/y=a/b
Since
c/d*((ad)/(bc))=(cad)/(dbc)
=a/b
x/y=(ad)/(bc)=a/b*d/c
Thus division is performed by the equation
(a)/(b)÷c/d= a/b*d/c=(a*d)/(b*c)
In other words, to divide by c/d, we simply invert this divisor, obtaining d/c, and multiply. For example,
1/5 ÷2/25=1/5*25/2=5/2
and
2/3÷4/-18=2/3*(-18)/4
= 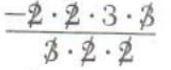
=-3/1=-3
Addition of rational numbers is performed according to the equation
a/b+c/b=(a+c)/b
For example,
1/5+3/5=(1+3)/5=4/5
and
1/6+(-4)/6=(1+(-4))/6
=-3/6=-1/2
In the case of addition of rational numbers with different denominators, the cancellation law is used to express the numbers as equivalent rational numbers with the same denominator.
For example,
1/2+1/3=(1*3)/(2*3)+(1*2)/(3*2)
=3/6+2/6=(3+2)/6=5/6
Here a common denominator is 2*3, simply the product of the denominators. The product of the denominators may always be used as a common denominator. However, the least common denominator (L..C.D), which is clearly the L.C.M. of the denominators, is easier to use. For example if we add 1/12 and 1/18, then L.C.M (12, 18)=36 is easier to use than 12*18=216.
Example 2.
Find 1/4+3/8+7/10.
Since 4=2*2
8=2*2*2
and 10=2*5
the L.C.D. is 2*2*2*5=40
Hence,
1/4+3/8+7/10=(1*10)/(4*10)+(3*5)/(8*5)+(7*4)/(10*4)
=10/40+15/40+28/40
=(10+15+28)/40=53/40
The definition for subtraction of rational numbers is the same as it is for natural numbers, namely, (a/b)-(c/d) is the rational number x/y such that
c/b+x/y=a/b
Since
c/b+((a-c)/b)=(c+(a-c))/b
=a/b
we have x/y=(a-c)/b
Hence, subtraction is performed by the equation
a/b-c/b=(a-c)/b
For example,
1/5-3/5=(1-3)/5=-2/5
As in the case of addition, if the rational numbers have different denominators, we find the L.C.D. and use the cancellation law to express them as equivalent rational numbers with the same denominator.
Example 3. Find 3/18-5/24.
Since 18=2*3*3
and 24=2*2*2*3
the L.C.D. is
2*2*2*3*3=72
Therefore, 3/18-5/24=(3*4)/(18*4)-(5*3)/(24*3)
=12/72-15/72
=(12-15)/72
=-3/72
=-1/24
Let’s see how our Number System solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
It is clear from the preceding definitions of addition, subtraction, multiplication, and division, that the set of rational numbers Q is closed under these operations. Furthermore, the set Q together with addition, subtraction, multiplication, and division, satisfies all of the laws that Z satisfies, namely, A.1-A.4, M.1-M.3, D.1 and D.2, as well as,
M.4 For each rational number r!=0, there is a unique rational number, denoted by 1/r, such that
r*1/r=1 (multiplicative inverse)
The rational number 1/r is called the multiplicative inverse of r, or the reciprocal of r.
The number system Q also satisfies the laws of computation that Z satisfies, C.1 through C.9, and in addition:
C.10 -m/n=m/-n=-(m/n)
C.11 -m/-n=m/n
For example,
-2/3=2/-3=-(2/3)
and -3/-5=3/5
The laws C.10 and C.11 follow easily from the definition of equality for example,
-m/-n=m/n
Since
-m(n)=(-n)m (C.6)
Example 4. Compute (a) 2/3(3/5+7/-2) (b) (-3/4-6/-2)÷(7/5)
(a) 2/3(3/5+7/-2)=2/3[3/5+(-7/2)] (C.10)
=2/3(3/5-7/2)
=2/3(6/10-35/10)
=2/3(-(29/10)
=-(1/3*29/5)
=-(29/5)
(b) (-3/4-6/-2)÷(7/5)=(-3/4+12/4)*5/7
=9/4*5/7
=45/28
Example 5. Compute (2/3-4+(-3)/2)/(1/3-5(2/7))
=(2/3-4+(-3)/2)/(1/3-5(2/7))=(4/6-24/6-9/6)/(7/21-30/21)
=((4-24-9)/6)/((7-30)/21)
=-29/6*21/-23
=203/46
1.4 Real Numbers
We have seen in the preceding sections how the natural numbers, the integers, and finally the rational numbers can be identified with points on a line and, conversely, certain points on the line can be identified with rational numbers. However, as we will soon see, there are points on the number line that as yet have no numbers assigned
to them.
During the 6th century B.C., Pythagoras, a famous Greek
mathematician, discovered the following formula for right triangles. If a,b, and c are the lengths of the sides of a right triangle with c being the longest side, then
c^2=a^2+b^2
where c^2=c*c . See Figure 4
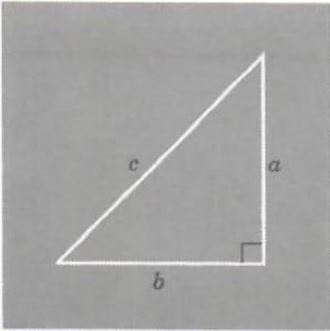
Figure 4
If we consider the right triangle where a and b are of length 1, then
c^2=1^2+1^2=2
that is, the length of the longest side is the number c such that c^2 = 2. We denote this number by the symbol root(2), which we call the square root of 2. This length corresponds to a point on the number line, however there is no rational number whose square is 2. For, if (p/q)^2 = 2, where p and q have no common factor, then
(p/q)^2=2
(9^2)/(q^2)=2/1
p^2=2q^2 (definition of equality in Q)
This equation tells us that p^2 is even and, therefore, p is even. Then for some integer r
p=2r
Substituting in the first equation we have
2q^2=(2r)^2=4r^2
Dividing by 2 we have
q^2=2r^2
Thus q^2 is even, and hence q is even. We have arrived at the conclusion that 2 is a common factor of p and q, contradicting the original assumption that p and q have no common factors. Therefore root(2) cannot be expressed as a ratio of integers, that is, it is not rational.
The fact that there is no rational number whose square is 2 was probably known to Pythagoras, but it is said that it disturbed him so much that he did not make the information known for fear t.hat it would discredit mathematicians in the eyes of the general public.
The above discussion shows that the collection of rational numbers is not closed under the operation of taking square roots. From the point of view of geometry this means that there are geometric figures whose sides cannot be measured exactly using only the collection of rational numbers. Also, on our number line this means that there are points that do not correspond to rational numbers. To fill in these gaps we must consider a larger collection of numbers, namely, the real numbers. There is a correspondence between the collection of real numbers and all the points on the number line, which we now refer to as the real number line. For example, root(2) corresponds to the point on the line obtained by taking the right triangle of sides 1, 1, and root(2) and placing it on the line as shown in Figure 5.
Given a point on the real number line, we may approximate the real number to which it corresponds by measuring the distance from the origin to the point. If we use a metric ruler our approximation will be a decimal accurate to a certain number of places. This decimal approximation is a rational number.
A completely logical treatment of real numbers was unknown until about 1870 when G. Cantor and R. Dedekind, two German mathematicians, gave a complete logical description and development.
The real numbers that are not rational are called irrational numbers. Irrational numbers are by no means scarce. Let root(n,a) denote the real number x such that x^n=a, n being a positive integer. If a is a positive integer that is not the nth power of an integer, then root(n,a) is irrational.
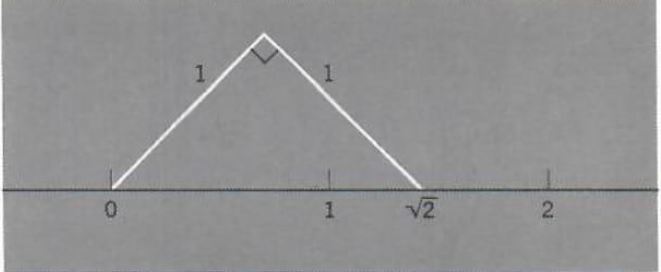
Figure 5.
For example, root(3),root(5), root(3,2),root(3,4),root(5,2),root(5,3),..., are all irrational numbers. Other irrational numbers may be found by applying the following two properties.
Property 1. If a rational number R is added to an irrational number {Iota}
then the sum S is again irrational.
Since S = R+{Iota}, it follows that {Iota}= S-R. Furthermore, if S were rational, then {Iota}= S-R would be rational, since the rational numbers are closed under subtraction. But {Iota} is irrational, hence S must also be irrational. Using property {Iota}, we see that the real numbers 3+root(2), 1+ root(3), and 1/2+ root(3,5), are irrational numbers.
Property 2. If a rational number R is multiplied by an irrational number {Iota}, then the product P is an irrational number.
This property follows from the fact that the rationals are closed under division, and we leave the proof as an exercise for the interested reader. From Property 2, the real numbers 2root(2),5root(3), and root(5,3/2) are irrational numbers.
There are many other irrational numbers that cannot be obtained by taking roots of rational numbers. For example PI, which is defined as the circumference of a circle divided by its diameter, is such an irrational number. From the above properties, the numbers 2PI,PI/3, and 1/2+ PI are also irrational numbers.
The collection of real numbers will be denoted by R. The relationships between the number systems N, W, Z, Q, and R are illustrated in Figure 6 below. Addition, subtraction, multiplication, and division
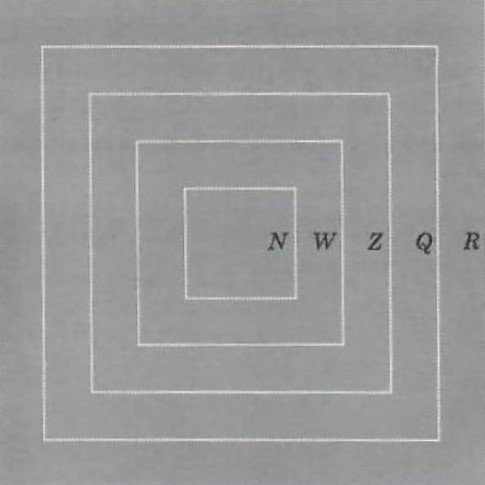
Figure 6.
(except by 0) can all be defined on R so that these operations are consistent with the operations on the set Q of rational numbers. Further more, the operations in R satisfy all of the basic laws of arithmetic that we had for Q, namely, A.1-A.4, M.1-M.4, D.1, D.2, as well as C.1—C.11.
The real numbers can be divided into three non-overlapping sets: the negative real numbers, zero, and the positive real numbers. A real number x is positive if it is to the right of 0 on the real number line, and negative if it is to the left of 0. We use the notation x > 0 if x is positive and x < 0 if x is negative. Inequalities will be studied in detail in Chapter 9.
An operation on real numbers which can be described in terms of positive and negative real numbers is that of computing the absolute value of a number. The absolute value of a is denoted by |a| and is defined by
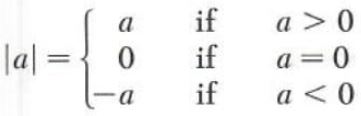
For example,
|2|=2
|-7|=-(-7)=7
|1/2|=1/2
|0|=0
and
|-root(2)|=root(2)
Note that for each real number a, a,|-a|=|a| = |a| is never negative.
Distance between two points on the line can be expressed by means of absolute values. In fact, if a and b are points on the real number line, then the distance between a and b, denoted by d(a, b), is given by
d(a,b)=|b-a|
Thus,
d(0,2)=|2-0|
=|2|
=2
d(0,-2)=|2-0|
=|-2|
=2
and
d(7/2,-4/3)=|-4/3-7/2|
=|-29/6|
=29/6
In particular, |a| represents the distance between a and 0 since
D(0,a)=|a-0|=|a|