Polynomials
2.1 Introduction
If a is any real number, then a^1=a,a^2=aa, a^3=aaa and, in general, if n is any positive integer, the symbol a^n is defined by the equation
a^n=aa...a (n factors)
In the symbol a^n,a is called Hie base and n is called the exponent. The term a^2 is read “a square,” a^3 is read “a cubed,” a^4 is read "a to the fourth power," and in general a^n is read “a to the nth power.”
A variable is a letter that takes on dmerent values from a given collection of real numbers during a given discussion. A constant is a symbol or letter that stands for just one particular real number during the discussion, even if we do not specify which real number it stands for. It is an agreed custom to use the first letters of the alphabet, such as a, b, c, d, ... , for constants and the latter letters of the alphabet. such as x, y, z, u, v, ..., for variables. Since there are only a finite number of letters in the alphabet we are sometimes forced to use subscripts on a single letter to distinguish between different constants. For example, a_0 is read “a-sub-nought" or “a-sub-zero," a, is read "a- sub-one,” and, in general, for n a positive integer a_n, is read “a-sub-n.” We certainly must not confuse subscripts with exponents.
By a monomial in the variables x, y, ... , z, we mean an expression
of the form
ax^(n)y^(m)...z^(v)
where n, m, ..., p are positive integers. For example, 7x^3y^2z^5 is a monomial in the variables x, y, and z. Constants are also referred to as monomials. A polynomial in the variables x, y,..., z is any sum of monomials in x, y,..., z. In particular, a binomial is the sum of two monomials and a trinomial is the sum of three monomials. A monomial appearing in a polynomial is referred to as a term of the polynomial.
By the degree of a monomial we shall mean the sum of the exponents of the variables, or if the monomial is a nonzero constant its degree is understood to be 0. Thus, the monomial 5 is of degree zero, 3x is of degree one, while 7x^3y^2z^5 is of degree ten. No degree is assigned to the monomial 0. Furthermore, while the term 7x^3y^2z^5 is of degree ten, it is also of degree three in x, two in y, and live in z. By the degree of a polynomial, we shall mean the degree of the monomial of highest degree appearing in the polynomial. Polynomials of degree one, two, or three often are called linear, quadratic, or cubic polynomials respectively.
Example 1. Find the degree, the degree in x, and the degree in y of the polynomial 7x^2y^3-4xy^2-x^3y+9y^4.
The terms of the polynomial are the monomials 7x^2y^3,-4xy^2-x^3y, and 9y^4.
| Degree in x | Degree in y | Degree | |
| 7x^2y^3 | 2 | 3 | 5 |
| -4xy^2 | 1 | 2 | 3 |
| -x^3y | 3 | 1 | 4 |
| 9y^4 | 0 | 4 | 4 |
Consequently the degree of the polynomial in x is 3, the degree in y is 4, and its degree is 5, as indicated in the table above.
Any collection of factors in a given monomial is called the coefficient of the remaining factors in the monomial. Thus in the monomial 3xy, 3 is the coefficient of xy, while 3y is the coefficient of x. The numerical factor of a monomial is referred to as the numerical coefficient or simply the coeificienl of the monomial. For example, 3 is the coefficient of 3x^2y, 1 is the coefiicient of x^2y^3, while -1 is the coefficient of -x
The leading coefficient of a. polynomial in a single variable is the coefficient of the term of highest degree. The constant term is the term with no variable factor. If we write the polynomial in descending powers of x, as
a_(n)x^n+a_(n-1)+x^(n-1)+...+a_1x+a_0
then the polynomial is of degree n, has leading coefficient a_n, and constant term a_0.
Example 2. What is the degree, leading coefficient, and constant term of each of the following?
(a) 3x^2-2x+1
(b) 7x-4x^3+3
(c) 2x-4x^2-x^5
(d) 5
| Degree | Landing Cofficient | Constant Term | |
| 3x^2-2x+1 | 2 | 3 | 1 |
| 7x-4x^3+3 | 3 | -4 | 3 |
| 2x-4x^2-x^5 | 5 | -1 | 0 |
| 5 | 0 | 5 | 5 |
The value of a polynomial in the variable x at the real number x = a is the real number obtained by replacing each occurrence of x in the polynomial by a. For example, the value of 2x^2- x + 7 at x = -3 is
2(-3)^2-(-3)+7=2*9+3+7
=18+3+7=28
The value of a polynomial in two or more variables is obtained in a similar way. We obtain the value of xy-x^2+ y^3 at x = 1, y = -2 by replacing each x with 1 and each y with -2:
(1)(-2)-(1)^2+(-2)^3=-2-1-8=-11
Thus the value of xy-x^2+y^3 at x=1, y=-2 is -11.
2.2 Addition and Subtraction of Polynomials
Since polynomials are expressions in one or more variables over the real numbers, the laws that we discussed in Chapter 1 may be used to develop techniques for adding, subtracting, multiplying, and dividing them.
The addition of two expressions, such as 2a and 4a, may be accomplished by a direct application of the distributive law. Thus,
2a+4a=(2+4)a=6a
Similarly,
7c-11c=(7-11)c=-4c
An expression of the form 2x + 3y cannot be put in any simpler form since in general x and y will denote two different quantities. We can, however, add two or more expressions of this kind in the following way.
Example 1. Add 2a+3b-4c and 6a-5b+2c.
Using the associative and commutative laws for addition as well as the distributive law we have
(2a+3b-4c)+(6a-5b+2c)
=(2a+6a)+(3b-5b)+(-4c+2c)
=(2+6)a+(3-5)b+(-4+2)c
=8a-2b-2c
In practice, when several expressions are to be added, the following method is sometimes helpful.
Example 2.
Add 3a-4ab^3+7c^3, 7ab-4a+5c^3, 2ab^2-4a+8c^3, and -5a+4ab-2ab^2+3c^3.
We write the expressions directly underneath one another in such a way that the terms containing the same letters appear in the same column as follows:
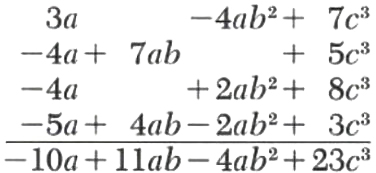
The bottom line is the final result, which is obtained by adding the respective columns.
We have already seen (Chapter 1) that subtraction of signed numbers may be accomplished by addition after changing the sign of the number to be subtracted. This is exactly what we do when we subtract polynomials.
Example 3.
Subtract 3x-2s+t from 4x+s-2t
(4x+s-2t)-(3x-2s+t)
=4x+s-2t-3x+2s-t
=(4x-3x)+(s+2s)+(-2t-t)
=x+3s-3t
Example 4.
From the sum of 2a + 7b - 15c and 60 - 4b + c subtract the sum of a-b+2c and -2a+6b-3c.
Since subtracting the sum of a - b + 2c and --2a+6b-3c is the same as subtracting each expression separately, we simply change all the signs of the last two expressions and add.
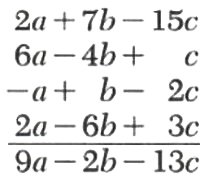
We handle grouping with parentheses the same way that we handled it with signed numbers in Section 1.2.
Example 5.
Simplify 8b-{7a-[(a-3b)-(2a+5b)]}.
8b-{7a-[(a-3b)-(2a+5b)]}
=8b-{7a-[a-3b-2a-5b]}
=8b-{7a+[-a-8b]}
=8b-{7a+a+8b}
=8b-{8a+8b}
=-8a
Let’s see how our Polynomials solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.
Example 6.
Rewrite the expression x-2y+ z-5 with the last three terms enclosed in parentheses preceded by a minus sign.
x-2y+z-5=x-(2y-z+5)
2.3 Multiplication of Polynomials
When multiplying monomials in which the variable x appears, we obtain products of the form x^(m)x^(n). The total number of factors of x in this product is m + n, so that we have the following law of exponents:
x^(m)x^(n)=x^(m+n)
For example,
x^(2)x^(7)=x^(2+7)=x^9
In order to multiply two or more algebraic expressions together we must make use of the above law as well as the laws of real numbers from Chapter 1.
Example 1.
Simplify (-3x^2y^3z)(2x^4yz^3).
(-3x^2y^3z)(2x^4yz^3)
=(-3*2)(x^2x^4)(y^3y)(z*z^3)
=-6x^6y^4z^4
In particular we make use of the distributive laws when we multiply two multinomials, as is illustrated in the following examples.
Example 2.
Multiply (x^3+2x^2-x+2) by (2x)
(x^3+2x^2-x+2)(2x)
=x^3(2x)+2x^3(2x)-x(2x)+2(2x)
=2x^4+4x^3-2x^2+4x
Example 3.
Multiply 3x^2+x-5 by x+2.
(3x^2+x-5)(x+2)
=3x^2(x+2)+x(x+2)-5(x+2)
=3x^2(x)+3x^2(2)+x(x)+x(2)-5(x)-5(2)
=3x^3+6x^2+x^2+2x-5x-10
=3x^3+7x^2-3x-10
From Example 3 we see that the terms in the product of one polynomial by another are obtained by multiplying each term in the first factor by each term in the second. With a little experience we will be able to skip the steps that use the distributive laws, simply writing down all the products. This is illustrated in the next two examples.
Let’s see how our polynomial solver Multiplies this and similar problems. Click on "Solve Similar" button to see more examples.
Example 4.
Multiply 2x+3 by x-5
(2x+3)(x-5)
=2x(x)+2x(-5)+2(x)+3(-5)
=2x^3-10x+3x-15
=2x^3-7x-15
Example 5.
Multiply 2x+y by x+2y-3.
(2x+y)(x+2y-3)
=2x^2+4xy-6x+xy+2y^2-3y
=2x^2+5xy+2y^2-6x-3y
2.4 Division of Polynomials
In order to divide one polynomial by another, we first must be able to divide one monomial by another. When dividing one monomial in at by another we must consider expressions of the form x^(m)÷x^(n) where m > n. This quotient is x^(m-n) since x^(m-n)x^n=x^m. Also if m = n, then x^m÷x^n = 1. This can be summarized as another law of exponents:
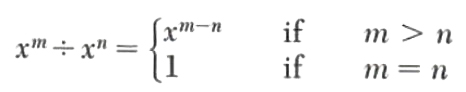
For example,
x^7÷x^2=x^(7-2)=x^5
Since
x^5x^2=x^(5+2)=x^7
Example 1.
Divide 8x^4y^2z^3 by 2x^2yz.
We use the notation of long division, which is what we will find convenient for dividing one polynomial by another.
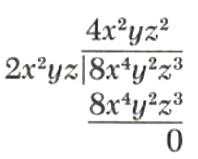
Thus,
8x^4y^2z^3÷2x^2yz=4x^2yz^3
The next example recalls the method of long division for integers.
Example 2.
Divide 492 by 8.
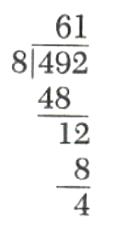
This gives us the equality
492=(61)(8)+4
Recall that 492 is called the dividend, 8 the divisor, 61 the quotient, and 4 the remainder. Note the division process terminates when the remainder is less than the divisor.
The division of one polynomial by another is carried out in a similar manner. Here the division terminates when the degree of the remainder is less than the degree of the divisor, or when the remainder is zero.
Example 3.
Divide -3x+2x^2+5 by x-1.
Step 1. Arrange both polynomials in descending powers of x, and write as follows.
![]()
Step 2. Divide x into 2x^2.
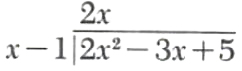
Step 3. Multiply x-1 by 2x and subtract from 2x^2-3x+5.
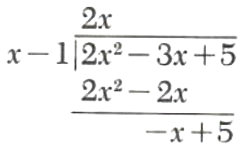
Since the degree of the remainder, -x+5, is not less than the degree of the divisor, x-1, we repeat the process.
Step 4. Divide x into -x.
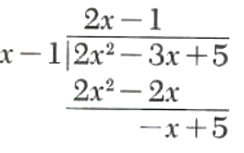
Step 5. Multiply x-1 by -1 and subtract from -x+5.
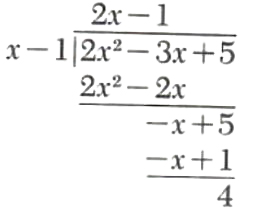
The remainder, 4, has degree 0, and Hie divisor, x- 1, has degree 1 Therefore, the division terminates.
Step 6. The result of this division is presented by the equation
(dividend) = (quotient)(divisor) + (remainder)
which in this example is
2x^2-3x+5=(2x-1)(x-1)+4
Example 4.
Divide 3x^3-2x+5 by x^2+x+1.
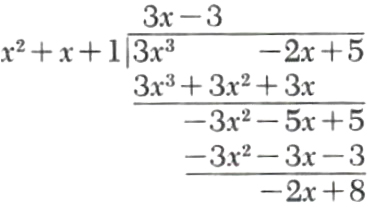
Since the degree of the remainder, -2x+8, is less than the degree of the divisor, x^2+x + 1, the process terminates. The result is
3x^2-2x+5=(3x-3)(x^2+x+1)-2x+8.
Example 5.
Divide 3x^3+2x^2-1 by 2x+7.
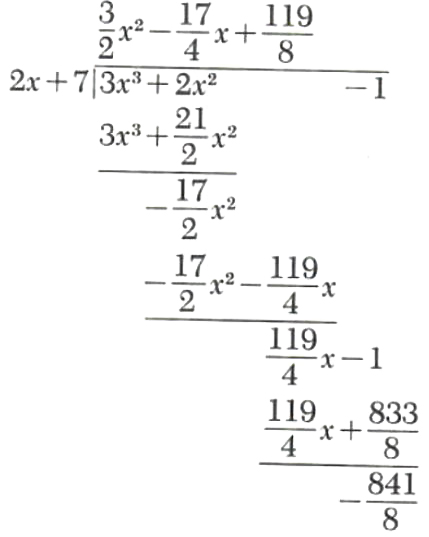
Thus,
3x^3+2x^2-1=(3/2x^2-17/4x+119/8)(2x+7)-841/8
Example 6.
Divide x^3+a^3 by x-a
To perform this division we treat these polynomials as polynomials in the single variable x.
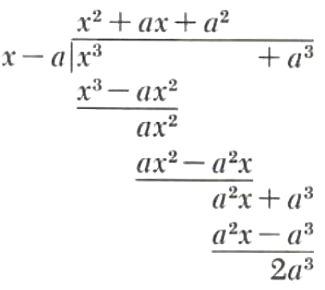
Thus,
x^3+a^3=(x^2+ax+a^2)(x-a)+2a^3