Rational expressions

An expression that is the quotient of two algebraic expressions (with denominator not 0) is called a fractional expression.  The most common fractional expressions are those that are the quotients of two polynomials; these are called rational expressions.  Since fractional expressions involve quotients, it is important to keep track of values of the variable that satisfy the requirement that no denominator be0. For example, x != -2 in the rational expression:

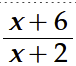
because replacing x with -2 makes the denominator equal 0.  Similarly, in

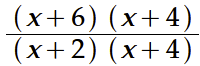
x!=-2 and x!= -4

The restrictions on the variable are found by determining the values that make the denominator equal to zero. In the second example above, finding the values of x that make (x + 2)(x + 4) = 0 requires using the property that ab = 0 if and only if a = 0 or b = 0,  as follows.

(x+2)(x+4)=0

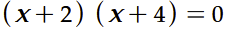
x+2=0 or x+4=0

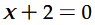
x=-2 or x=-4

Just as the fraction 6/8 is written in lowest terms as 3/4, rational expressions may also be written in lowest terms. This is done with the fundamental principle.

Example 1

Write each expression in lowest terms.

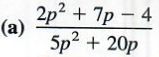
Factor the numerator and denominator to get

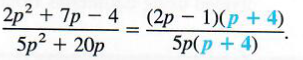
By the fundamental  principle,

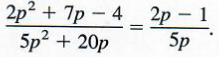
In the original expression p cannot be 0 or -4, because

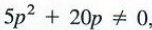
So this result is valid only for values of p other than 0 and -4.   From now on, we shall always assume such restrictions when reducing rational expressions.

Now let's take a look at how our step-by-step fraction solver solves this problem:

Example 2

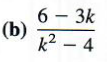
Factor to get

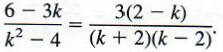
The factors 2 - k and k - 2 have opposite signs.  Because of this, multiply numerator and denominator by -1,   as follows.

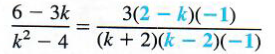
Since (k-2)*(-1)=-k+2  or 2- k,

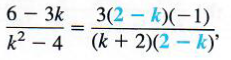
Giving

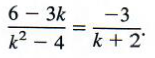
Working in an alternative way would lead to the equivalent result

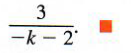
Our fraction calculator can solve this and many similar problems. If you would like a similar problem to be generated, click on solve similar button:

Caution            

Probably the most common error made in algebra is the incorrect use of the fundamental principle to write a fraction in lowest terms, Remember, the fundamental principle requires a pair of common factors, one in the numerator and one in the denominator. For example,

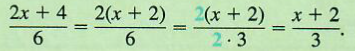
On the other hand

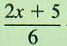
cannot be simplified further by the fundamental principle, because the numerator cannot be factored.