Simplification and Addition of Algebraic Fractions
Algebraic fractions are similar to arithmetic fractions in that both indicate
7.1 Simplification of Algebraic Fractions
From the properties of fractions, discussed before, we have a/b = ac/bc. The two algebraic fractions a/b and ac/bc are called equivalent fractions.
A fraction is in its lowest terms, or reduced, when the numerator and the denominator do not possess a common factor.
To reduce or simplify the algebraic fraction ac/bc to its lowest terms, we divide both numerator and denominator by their common factor, c, to get a/b. The a and the c in are factors of the numerator, not terms as in a + c. Also the b and the c are factor the denominator, not terms.
The fraction (a+c)/(b+c) cannot be reduced to any simpler form; it is not equal to either a/b or (a+1)/(b+1). Similarly,
![]()
but (5a+b)/(6a) = (5a)/(6a) + b/(6a) = 5/6+b/(6a)
To find the greatest common factor, GCF, of a set of polynomials, factor the polynomials completely and take all common factors, each to the least exponent to which that factor appears in any of the given polynomials.
To reduce to its lowest terms a fraction whose numerator and denominator are monomials, divide both numerator and denominator by their greatest common factor.
EXAMPLE Reduce (36a^3b^2c)/(54abc^3) to its lowest terms.
Solution The greatest common factor of the monomials 36a^3b^2c and 54abc^3 is 18abc. Dividing both numerator and denominator by 18abc, we get
(36a^3b^2c) /(54abc^3) = (2a^2b)/(3c^2)
Let’s see how our Algebraic solver solves this and similar expression. Click on "Solve Similar" button to see more examples.
EXAMPLE Reduce (36x^3y^6(x-2))/((20xy^3(x-2)^4 to its lowest terms
Solution The greatest common factor is 4xy^2(x-2).
Dividing both numerator and denominator by 4xy^2(x-2), we get
(36x^3y^6(x-2))/((20xy^2(x-2)^4 = (9x^2y^4)/(5(x-2)^3)
When either the numerator or the denominator or both are polynomials, factor them completely, determine their greatest common factor, and then divide them by that greatest common factor.
EXAMPLE Reduce (30x^2y^3-18xy^2)/(12x^2y^2) to ist lowest terms.
Solution (30x^2y^3-18xy^2)/(12x^2y^2) = (6xy^2(5xy-3))/(12x^2y^2)
Dividing both numerator and denominator by 6xy^2, we obtain
(30x^2y^3-18xy^2)/(12x^2y^2) = (6xy^2(5xy-3))/(12x^2y^2) = (5xy-3)/(2x)
EXAMPLE Reduce (24x^3y)/(36x^3y^2+48x^4y) to its lowest terms.
Solution (24x^3y)/(36x^3y^2+48x^4y) = (24x^3y)/(12x^3y(3y+4x))
Dividing both numerator and denominator by 12x^3y to obtain
(24x^3y)/(36x^3y^2+48x^4y) = (24x^3y)/(12x^3y(3y+4x)) = 2/(3y+4x)
EXAMPLE Reduce (2x^2+x-3)/(x^2-1) to its lowest terms.
Solution Factoring both numerator and denominator. we obtain
(2x^2+x-3)/(x^2-1) = ((2x+3)(x-1))/((x+1)(x-1))
Dividing both numerator and denominator by their greatest common factor, (x - 1). we get
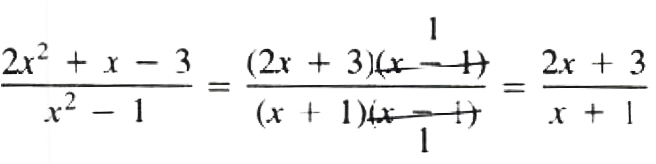
Note The fraction (2x+3)/(x+1) is in its lowest terms; the numerator and denominator do not possess a common factor.
Let’s see how our Algebraic solver solves this and similar expression. Click on "Solve Similar" button to see more examples.
Notes 1. a-b = -b+a = -(b-a)
2. (a-b)^2 = [-(b-a)]^2 = (b-a)^2
3. (a-b)^3 = [-(b-a)]^3 = -(b-a)^3
EXAMPLE (a-b)/(b-a) = -(b-a)/(b-a) = -1
EXAMPLE (a-1)^3/(1-a)^2 = -(1-a)^3/(1-a)^2 = -(1-a) = a-1
or (a-1)^3/(1-a)^2 = (a-1)^3/(a-1)^2 = a-1
Note The fraction (a+b)/(a-b) cannot be reduced to any simpler form, since a+b can never be written as a multiple of a-b.
Note also that
-a/+b = +a/-b = -(a/b)
EXAMPLE Reduce (8x^2-14x+3)/(2-7x-4x^2)
Solution (8x^2-14x+3)/(2-7x-4x^2) = ((4x-1)(2x-3))/((2+x)(1-4x) [(4x-1) = -(1-4x)]
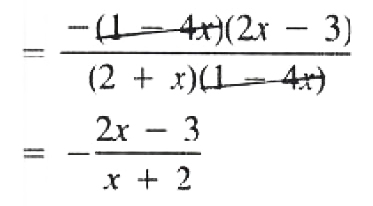
EXAMPLE Reduce (x^2 - 5x +6)/(2-3x+x^2
Solution (x^2 - 5x +6)/(2-3x+x^2
=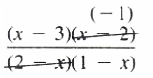
= -(x-3)/(1-x) = (3-x)/(1-x) or, = (x-3)/(x-1)
7.2 Addition of Algebraic Fractions
Addition of algebraic fractions is similar to addition of fractions in arithmetic. We will start by discussing adding algebraic fractions with like denominators and then extend the discussion to addition of algebraic fractions with unlike denominators.
Fractions with Like Denominators
Addition of fractions with like denominators is defined earlier by the relation
a/c+b/c = (a+b)/c
This shows that the sum of two fractions with the same denominator is a fraction whose numerator is the sum of the numerators and whose denominator is the common denominator.
EXAMPLE Combine 3/x+2/x.
Solution 3/x+2/x = (3+2)/x = 5/x
Remark To avoid making mistakes in adding the numerators, it is advisable to enclose the numerators in parentheses, apply the distributive law, and than combine.
Remark After combining the two fractions into one fraction, combine like terms, and then reduce the new fraction.
EXAMPLE Combine (x+3)/(2x^2)+(x-3)/(2x^2)
Solution (x+3)/(2x^2)+(x-3)/(2x^2) = ((x+3)+(x-3))/(2x^2)
=(x+3+x-3)/(2x^2)
=(2x)/(2x^2) = 1/x
Let’s see how our Algebraic equation solver solves this and similar expressions. Click on "Solve Similar" button to see more examples.
EXAMPLE Combine 4/(x+2) - (2x)/(x+2)
Solution 4/(x+2) + (2x)/(x+2) = (4+2x)/(x+2)
=(2(2+x))/(x+2) =2
EXAMPLE Combine(x^2-2)/(x^2+x-2) - (x^2-2x)/(x^2+x-2)
Solution (x^2-2)/(x^2+x-2) - (x^2+2x)/(x^2+x-2) = ((x^2-2)-(x^2-2x))/(x^2+x-2)
=(x^2-2-x^2+2x)/(x^2+x-2) - (2x-2)/(x^2+x-2)
=(2(x-1))/((x+2)(x-1) = 2/(x+2)
EXAMPLE Combine (x^2+9x)/(4x^2-11x-3) - (5x^2-3x)/(4x^2-11x-3)
Solution (x^2+9x)/(4x^2-11x-3) - (5x^2-3x)/(4x^2-11x-3)
=((x^2+9x)-(5x^2-3x))/(4x^2-11x-3)
=(x^2+9x-5x^2-3x)/(4x^2-11x-3)
=(12x-4x^2)/(4x^2-11x-3) =(4x(3-x))/((4x+1)(x-3)
=(-4x(x-3))/((4x+1)(x-3) = -(4x)/(4x+1)
Remark The rule for combining two fractions can be extended to any number of fractions
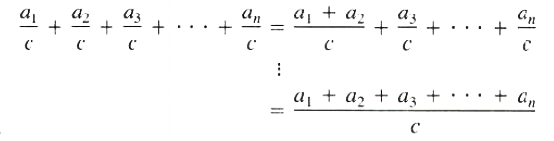
EXAMPLE Combine (4x^2+x)/(2x^2-5x-12) - (2x^2+15x)/(2x^2-5x-12) + (5x^2-14x)/(2x^2-5x-12)
Solution (4x^2+x)/(2x^2-5x-12) - (2x^2+15x)/(2x^2-5x-12) + (5x^2-14x)/(2x^2-5x-12)
=((4x^2+x)-(2x^2+15x)+(5x^2-14x))/(2x^2-5x-12)
=(4x^2+x-2x^2-15x+5x^2-14x)/(2x^2-5x-12)
=(7x^2-28x)/(2x^2-5x-12)
=(7x(x-4))/((2x-3)(x-4))
=(7x)/(2x+3)
Least Common Multiple of Polynomials
To find the least common multiple (LCM) of a set of numbers, factor the numbers into their prime factors and Write them in the exponent form. Take all the bases each to the highest exponent.
DEFINITION
A polynomial P is the least common multiple of a set of polynomials if
1. each polynomial in the set divides P, and
2. any polynomial divisible by all the polynomials in the set is also divisible by P.
To find the LCM of a set of polynomials, factor the polynomials completely and take distinct factors. each to the largest exponent to which it appears in any of the given polynomials.
EXAMPLE Find the LCM of x^2y,xy^3, and y^2z,
Solution The literal factors are x, y, and z.
The greatest power of x is 2, of y is 3, and of z is 1.
Hence LCM = x^2y^3z
EXAMPLE Find the LCM of 60x^3,72y^2 and 80xy,
Solution 60 = 2^2*3*5
72 = 2^3*3^2
80 = 2^4*5
Hence the LCM of the spicific numbers = 2^4*3^2*5 = 720.
The LCM of the monomials = 720x^3y^2.
EXAMPLE Find the LCM of x(x-2),(x-3)(x-2), and (x-2)^2
Solution The distinct factors are x,(x-2), and (x-3).
The greatest power of x is 1, of (x-2), is 2, and of (x-3) is 1.
Hence LCM = x(x-2)^2(x-3)
Note that the LCM of (x-3) and (x-5) is (x-3)(x-5).
EXAMPLE Find the LCM of x^2-x and x^2-1
Solution First factor each polynomial completely.
x^2-x = x(x-1)
x^2-1 = (x+1)(x-1)
Hence LCM = x(x-1)(x+1)
EXAMPLE Find the LCM of 2x^2+3x-2 and 2x^2-7x+3
Solution 2x^2+3x-2 = (2x-1)(x+2)
2x^2-7x-3 = (2x-1)(x-3)
Hence LCM = (2x-1)(x+2)(x-3)
EXAMPLE Find the LCM of 9x^2-4 and 9x^2+12x+4
Solution 9x^2-4 = (3x+2)(3x-2)
9x^2+12x+4 = (3x+2)(3x+2) = (3x+2)^2
Hence LCM = (3x+2)^2(3x-2)
EXAMPLE Find the LCM of 2x^2-3x+1,1-x^2, and 2x^2+x-1.
Solution 2x^2-3x+1 = (2x-1)(x-1)
1-x^2 = (1+x)(1-x)
2x^2+x-1 = (2x-1)(x+1)
Since (1-x) = -(x-1), we can write either (1-x) as -(x-1), or (x-1) as -(1-x)
Remember that 1+x = x+1
Hence 2x^2-3x+1 = (2x-1)(x-1)
1-x^2 = -(x+1)(x-1)
2x^2+x-1 = (2x-1)(x+1)
Thus LCM = (2x-1)(x-1)(x+1)
Fractions with Unlike Denominators
Fractions can be added only when their denominators are alike. When the denominators are not alike, find the least common multiple of the denominators, called the least common denominator, LCD. Change each fraction to an equivalent fraction having the LCD as a denominator, by the rule
a/b = ac/bc
and then combine. The sum of algebraic fractions having unlike denominators is therefore a fraction whose numerator is the sum of the numerators of the equivalent fractions and whose denominator is the LCD. The final fraction must be reduced to lowest terms.
EXAMPLE Combine 7/(2x)+6/x^2-2/(3x)
Solution The LCD = 6x^2
We write equivalent fractions with denominational 6x^2 and then combine.
7/(2x)+6/x^2-2/(3x) = (7(3x))/(2x(3x))+(6(6))/(x^2(6))-(2(2x))/(3x(2x))
= (7(3x))/(6x^2)+(6(6))/(6x^2)-(2(2x))/(6x^2)
= (7(3x)+6(6)-2(2x))/(6x^2)
= (21x+36-4x)/(6x^2) = (17x+36)/(6x^2)
Let’s see how our Algebraic math solver solves this and similar expressions. Click on "Solve Similar" button to see more examples.
EXAMPLE (x+2)/(4x)-(3x-1)/(6x^2)
Solution The LCD = 12x^2
(x+2)/(4x)-(3x-1)/(6x^2) = (3x(x+2))/(3x(4x))-(2(3x-1))/(2(6x^2))
= (3x(x+2))/(12x^2)-(2(3x-1))/(12x^2)
= (3x(x+2)-2(3x-1))/(12x^2)
= (3x^2+6x-6x+2)/(12x^2) = (3x^2+2)/(12x^2)
EXAMPLE Combine and simplify x/(x+3)+2/(x-2)
Solution The LCD = (x+3)(x-2)
Writing equivalent fractions with denominator (x+3)(x-2) and then combining, we get
x/(x+3)+2/(x-2) = (x(x-2))/((x+3)(x-2))+(2(x+3))/((x-2)(x+3))
=(x(x-2)+2(x+3))/((x+3)(x-2))
=(x^2-2x+2x+6)/((x+3)(x-2))
= (x^2+6)/((x+3)(x-2))
EXAMPLE Combine and simplify (9x-20)/(x^2+x-12)-(6x-13)/(x^2-x-6)
Solution We first factor the denominators.
(9x-20)/(x^2+x-12)-(6x-13)/(x^2-x-6)
= (9x-20)/((x+4)(x-3))-(6x-13)/((x-3)(x+2))
The LCD = (x+4)(x-3)(x+2)
Instead of writing equivalent fractions with denominators equal to the LCD, and then combining the numerators of the fractions, we write one fraction with the LCD as the denominator. Divide the LCD by the denominator of the first fraction, and then multiply the resulting quotient by the numerator of that fraction to get the first expression of the numerator. Repeat the process for each fraction. connecting them by the signs of the corresponding fractions.
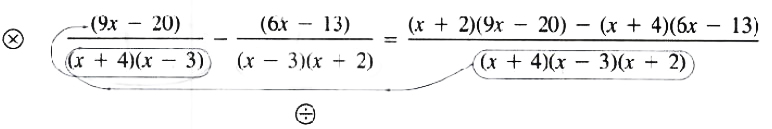
The numerator is not in factored form; thus we cannot reduce. Be sure to put the product in parentheses preceded by the correct sign.
=((9x^2-2x-40)-(6x^2+11x-52))/((x+4)(x-3)(x+2))
=(9x^2-2x-40-6x^2-11x+52)/((x+4)(x-3)(x+2))
=(3x^2-13x+12)/((x+4)(x-3)(x+2))
= ((3x-4)(x-3))/((x+4)(x-3)(x+2))
=(3x-4)/((x+4)(x+2))
EXAMPLE Combine and simplify
(x+2)/(2x^2-x-1)-(3x-2)/(2x^2+9x+4)+5/(4-3x-x^2)
Solution (x+2)/(2x^2-x-1)-(3x-2)/(2x^2+9x+4)+5/(4-3x-x^2)
=(x+2)/((2x+1)(x-1))-(3x-2)/((2x+1)(x+4))+5/((4+x)(1-x))
Take the LCD = (2x+1)(x-1)(x+4)
=(x+2)/((2x+1)(x-1))-(3x-2)/((2x+1)(x+4))+5/(-(4+x)(x-1))
=(x+2)/((2x+1)(x-1))-(3x-2)/((2x+1)(x+4))-5/((4+x)(x-1))
=((x+4)(x+2)-(x-1)(3x-2)-5(2x+1))/((2x+1)(x-1)(x+4))
=((x^2+6x+8)-(3x^2-5x+2)-10x-5)/((2x+1)(x-1)(x+4))
=(x^2+6x+8-3x^2+5x-2-10x-5)/((2x+1)(x-1)(x+4))
=(1+x-2x^2)/((2x-1)(x-1)(x+4))
= ((1+2x)(1-x))/((2x+1)(x-1)(x+4))-(-(1+2x)(x-1))/((2x+1)(x-1)(x+4))
= -(1/(x+4))
EXAMPLE Combine and simplify
(5x-4)/(2x^2-11x-6)+(3x+4)/(2x^2+7x+3)-(3x)/(x^2-3x-18)
Solution (5x-4)/(2x^2-11x-6)+(3x+4)/(2x^2+7x+3)-(3x)/(x^2-3x-18)
=((5x-4))/((2x+1)(x-6))+((3x+4))/((2x+1)(x+3))-(3x)/((x+3)(x-6))
=((x+3)(5x-4)+(x-6)(3x+6)-3x(2x+1))/((2x-1)(x-6)(x+3))
=((5x^2+11x-12)+(3x^2-14x-24)-(6x^2+3x))/((2x+1)(x-6)(x+3))
=(5x^2+11x-12+3x^2-14x-24-6x^2-3x)/((2x+1)(x-6)(x+3))
=(2x^2-6x-36)/((2x+1)(x-6)(x+3))
=(2(x^2-3x-18))/((2x+1)(x-6)(x-3)
=(2(x+3)(x-6))/((2x+1)(x-6)(x+3)
= 2/(2x+1)
Let’s see how our Algebraic math solver solves this and similar expressions. Click on "Solve Similar" button to see more examples.