Simplifying Radicals

Radicals were introduced in previous tutorial when we discussed real numbers. For example, root(25) = 5, and root(2) = 1.4142135 ... (an infinite nonrepeating decimal). We are now interested in developing techniques that will aid in simplifying radicals and expressions that contain radicals. In this text, we will deal only with radicals that are square roots. Other radicals, such as cube roots 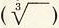and fourth roots , will be discussed in later algebra courses.
        The following two properties of radicals are basic to the discussion.

Thus,

              root(144)=root(36)*root(4)=6*2=12

and         root(9/25)=root(9)/root(25)=3/5

To simplify root(450), we can write 

root(450)=root(25*18)=root(25)root(18)=5root(18)

Is 5root(18) the simplest form of root(450)? The answer is no, because root(18) has a square number factor, 9, and

root(18)=root(9)root(2)=3root(2) .

We can write

     root(450)=root(25*18)=root(25)*root(9)*root(2)=5*3*root(2)=15root(2)

or root(450)=root(225*2)=root(225)*root(2)=15root(2)

          In simplifying a radical, try to find the largest square factor of the radicand. A radical is considered to be in simplest form when the radicand has no square number factor.

Examples

Simplify the following radicals.

1. root(24)     Factor 24 so that one factor is a square number.

    root(24)=root(4*6)=root(4)*root(6)=2root(6)

2. root(72)     Find the largest square factor you can before simplifying.

    root(72)=root(36*2)==root(36)*root(2)=6root(2)

Or, if you did not notice 36 as a factor, you could write

    root(72)=root(9*8)=root(9)*root(8)=3root(4*2)=3*root(4)*root(2)=3*2*root(2)=6root(2)

3.  -root(288)

    -root(288)=-root(144*2)=-root(144)*root(2)=-12root(2)

4.  root(75/4)

     root(75/4)=root(75)/root(4)=root(25*3)/2=(root(25)*root(3))/2=(5root(3))/2

5.  {3+root(18)}/3

     (3+root(18))/3=(3+root(9*2))/3=(3+root(9)*root(2))/3=(3+3root(2))/3 

                      = 3/3+(3root(2))/3=1+root(2)