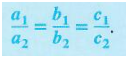Special cases involving linear systems of equations

Solving an inconsistent system by elimination

Solve the system

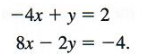
The variable x can be eliminated by multiplying both sides of the first equation by 2 and then adding.

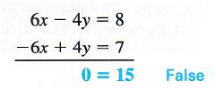
Both variables were eliminated here, leaving the false statement 0 = 15,  a signal that these two equations have no solutions in common. The system is inconsistent, and the solution  set is empty.  In slope-intercept form, the equations would show that the graphs are parallel  lines because they have the same slope but different y-intercepts.

Example 2:

Solve the system

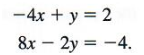
Eliminate  x by multiplying  both sides  of the first equation by 2 and then adding it to the second equation.

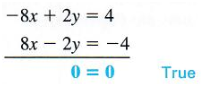
This true statement, 0 = 0, indicates  that a solution of one equation is also a solution of the other, so the solution set is an infinite set of ordered pairs. The graphs of the equations are the same line, since  the slopes  and j-intercepts are equal. The two equations are dependent.

We will write the solution of a system of dependent equations as an ordered pair by expressing x in terms of y as follows. Choose either equation and solve for x. Choosing the first equation gives

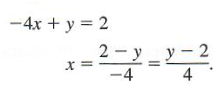
We write the solution set as

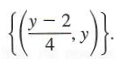
By selecting values for y  and calculating the corresponding values for x, individual  ordered pairs  of the  solution  set can  be found. For example,  if  y  = -2, x = (-2  -   2)/4 = -1   and the ordered pair ( -  1,   - 2) is a solution.

NOTE : In the previous example we wrote the solution set in a form with the variable y arbitrary. However, it would be acceptable to write the ordered pair with x arbitrary. In this case, the solution  set would be written

{(x, 4x + 2)}.

By selecting values for x and solving  for y in  the ordered pair above, individual solutions can be found.  Verify that (-1,   -2) is  a solution.

Special Cases for Systems

Consider the system of equations

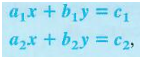
with a_1, b_1, c_1, a_2, b_2 and c_2 not equal to 0. The graphs of the equations are parallel lines and the system is inconsistent if

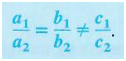
The graphs of the equations are the same line and the equations are dependent if