Factoring
3.1 Prime Factors for Polynomials
The student should begin this chapter with a review of the idea of factoring integers. which was discussed in Chapter 1.
A polynomial P is said to he a factor or divisor of a polynomial R if there exists a polynomial Q such that
R=PQ
Note that Q is also a divisor of R.
In this chapter we will agree that our polynomials are to have only integral coefficients. For example,
x^2-1=(x-1)(x+1)
and therefore x^2-1 has factors x-1 and x+1. But, even though
x^2-6=(x-root(6))(x+root(6))
we do not consider x-root(6) and .x+√6 as factors of x^2-6 since they fail tn have integral coefficients. A given polynomial with integral coefficients is said to he prime if it has no factors other than plus or minus one and plus or minus itself, subject to the above restrictions. A polynomial is said to be factored completely when it is expressed as a product of prime factors.
When we are obtaining factors of polynomials we must make allowances for changes in sign. Since
x^2-1=(x-1)(x+1)
=(-1)(-x+1)(x+1)
and we do not want to distinguish between these factorization, we will agree that if the factors differ only by a multiple of -1, they will be considered to be equivalent. With this understanding the following is true: Every polynomial can be expressed uniquely as the product of prime factors apart form the order in which they are written and subject to trivial changes in sign. This is known as the Unique Factorization Theorem for Polynomials.
The problem of finding all of the prime factors of a given polynomial is, in general, a difficult one. In this chapter we consider techniques for finding factors of certain types of polynomials. In order to find the prime factors of a given polynomial we must be able to tell whether or not a polynomial is prime. One type of polynomial that is always prime is a polynomial of first degree, ax + b, for which the only common factors of a andb are +-1. For example, 3x+4 is prime since 3 and 4 have only +-1 as common factors, while 4x + 6 is not prime since 2 is a common factor of 4 and 6. In fact, 4x +6 = 2(2x + 3).
Using long division we can determine if a given polynomial is a factor of another polynomial. This is the case if and only if the remainder is zero when we divide the second polynomial by the first.
Example 1. Is x-2 a factor of x^3-8?
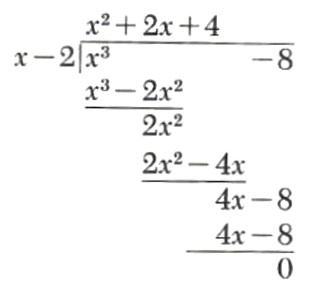
The remainder is 0, hence x-2 is a factor. In fact,
x^3-8=(x^2+2x+4)(x-2)+0
=(x^2+2x+4)(x-2)
3.2 Factors Common to All Terms
The method of factoring a common term from a given polynomial is based on the distributive laws, which we recall from Chapter 1,
namely,
ab+ac=a(b+c)
ac+bc=(a+b)c
Example 1. Factor 2x^2+3xy.
The factor common to each term is x. Thus,
2x^2+3xy=x(2x+3y)
Notice that we can always check the factorization by multiplying the factors together and comparing the result with the original polynomial.
Example 2. Factor 5a^2x^2y^3-25ax^7y^2z.
The common factor is 5ax^2y^2 ,Therefore
5a^2x^2y^3-25ax^7y^2z=5ax^2y^2(ay-5x^5z)
Example 3. Factor (a+b)x-(a+b)y+(a+b)z.
The common factor is (a + b) and therefore
(a+b)x-(a+b)y+(a+b)z=(a+b)(x-y+z)
If, in Example 3, the polynomial had been written as
ax+bx-ay-by+az+bz
then no factor is common to all terms. It takes a certain amount of experience to see that the terms can be grouped so that each group has a common factor. For example ax+bx-ay-by+az+bz can be grouped to obtain the expression in Example 2, namely,
ax+bx-ay-by+az+bz=(a+b)x-(a+b)y+(a+b)z
Sometimes there is more than one way to group the terms of 2. given polynomial. For example, the above polynomial can be grouped in another way.
ax+bx-ay-by+az+bz=ax-ay+az+bx-by+bz
=a(x-y+z)+b(x-y+z)
=(a+b)(x-y+z)
Example 4. Factor 20x^2+15xy+8xz+6yz.
20x^2+15xy+8xz+6yz=5x(4x+3y)+2z(4x+3y)
=(5x+2z)(4x+3y)
Example 5. Factor 2x^4+4x^3y-2x^2y^3-4xy^4.
We first observe that 2x is a factor of each term so that
2x^4+4x^3y-2x^2y^3-4xy^4=2x(x^3+2x^2y-xy^3-2y^4)
We now consider x^3+2x^2y-xy^3-2y^4. We factor x^2 from first two terms and y^3 from the last two terms obtaining
x^3+2x^2y-xy^3-2y^4=x^2(x+2y)-y^3(x+2y)
Each of the two terms has (x + 2y) as a factor, so that
x^2(x+2y)-y^3(x+2y)=(x^3-y^3)(x+2y)
Thus,
2x^4+4x^3y-2x^3y^3-4xy^4
=2x(x^3+2x^2y-xy^3-2y^4)
=2x[x^2(x+2y)-y^3(x+2y)
=2x[(x^2-y^3)(x+2y)
=2x(x^2-y^3)(x+2y)
Let’s see how our step by step solver factorizes this and similar problems. Click on "Solve Similar" button to see more examples.
Example 6. Factor 2u^2x-uwx+3uv+6u^2+uvx-3uw.
2u^2x-uwx+3uv+6u^2+uvx-3uw
=u(2ux+wx+3v+6u+vx-3w)
=u[(2ux+6u)+(vx+3v)-(wx+3w)
=u[2u(x+3)+v(x+3)-w(x+3)
=u(2u+v-w)(x+3)
3.3 The Difference of Two Squares
We observe that
(a-b)(a+b)=a^2-ba+ab-b^2=a^2-b^2
For purposes of factoring we have
a^2-b^2=(a-b)(a+b)
Example 1. Factor y^2-9.
y^2-9=y^2-3^2=(y-3)(y+3)
Example 2. Factor 16x^2-9y^4.
16x^2-9y^4=(4x)^2-(3y^2)^2= (4x-3y^2)(4x+3y^2)
Example 3. Factor 8u^3z^2-2uz^4.
8u^3z^2-2uz^4=2uz^2(4u^2-z^2)= 2uz^2(2u-z)(2u+z)
Example 4. Factor u^4-16v^4.
u^4-16v^4
=(u^2)^2-(4v^2)^2
=(u^2-4v^2)(u^2+4v^2)
Since u^2-4v^2is also the difference of two squares we have
u^2-16v^2
=[u^2-(2v)^2](u^2+4v^2)
=(u-2v)(u+2v)(u^2+4v^2)
We can also combine this new idea with the idea of grouping terms to obtain a common factor as is illustrated in the following example.
Example 5. Factor x^2-y^2+4x-4y.
x^2-y^2+4x-4y
=(x^2-y^2)+(4x-4y)
=(x-y)(x+y)+4(x-y)
=(x-y)(x+y+4)
3.4 Polynomials of the Form x^2+bx+c
Suppose that x^2+bx+c can be factored into the product of two first degree polynomials; that is,
x^2+bx+c = (x+r)(x+s)
Since
(x+r)(x+s) = x^2+rx+sx+rs
=x^2+(r+s)x+rs
then
x^2+bx+c = x^2+(r+s)x+rs
Comparing coefficients we see that r and s must satisfy the two equations
(1) rs=c and r+s=b
Therefore the problem of factoring x^2+bx+c, where b and c are integers, can be solved by finding integers r and s that satisfy the two equations in (1).
To find integers r and s that satisfy equations (1), we first find all pairs of integers whose product is c, and then select the pair whose sum is b, if such a pair exists.
Example 1. Factor x^2+5x+6.
The possible factorization of 6 are 6*1 and 3*2. In this case it is easy to see that we want 3*2 since 3+2 = 5. Thus,
x^2+5x+6=(x+2)(x+3)
Example 2. Factor x^2-2x-15.
Here the factors of -15 must be of opposite sign and therefore the possibilities are (15)(- 1), (-15)(1), (5)(-3), and (-5)(3). Since the sum of -5 and 3 is -2, we have
x^2-2x-15 = (x-5)(x+3)
Example 3. Factor x^2+2x+3
Since 3 is prime its only factorization is 3*1. Since the sum of these factors is not 2, x^2+2x +3 is prime.
Example 4. Factor x^2-ax-2a^2.
Since the coefficient of x is -a, the only factorization of -2a^2 that we need to consider are (-2a)(a) and (2a)(-a). Observing that -2a+a=-a, we have
x^2-ax-2a^2=(x-2a)(x+a)
In the next two examples we illustrate how this technique may be combined with the ones we have used previously.
Example 5. Factor a^2-ab-2b^2+4a+4b.
Since 4a+4b has a factor a+b, we hope that a+b is also a factor of a^2-ab-2b^2. The only factorization of a^2 with a as one factor is (a)(a) and the only factorization of -2b^2 with b as one factor is (-2b)(b) thus the other factor of a^2-ab-2b^2 would have to be a-2b. Thus,
a^2-ab-2b^2+4a+4b
=(a^2-ab-2b^2)+(4a+4b)
=(a+b)(a-2b)+4(a+b)
=(a+b)(a-2b+4)
Let’s see how our step by step solver factorizes this and similar problems. Click on "Solve Similar" button to see more examples.
Example 6. Factor a^4-5a^2+4.
Although this is not a quadratic in a, it is a quadratic in a^2, that is,
a^4-5a^2+4=(a^2)^2-5(a^2)+4
Since the coefficient of a^2 is negative, the two possible factorization of 4 are (-4) (-1) and (-2) (-2). Since (-4) + (-1) = -55, we have
a^4-5a^2+4=(a^2+4)(a^2-1)
Since each of the factors obtained is the difference of two squares we factor again obtaining
a^4-5a^2+4
=(a^2-4)(a^2-1)
=(a-2)(a+2)(a-1)(a+1)
3.5 Polynomials of the Form ax^2+bx+c
When the coefficient of x^2 is an integer other than 1, the process of factoring is more difficult. We see by direct multiplication that
(px+q)(rx+s)=prx^2+(ps+qr)x+qs
In comparing this with
ax^2+bx+c
we see that we must find four integers p, q, r, and s such that
pr=a
qs=c
ps+qr=b
Example 1. Factor 2x^2+7x+5.
Suppose 2x^2+7x+5=(px+q)(rx+s). To make sure that we consider all possibilities we arrange our work in tabular form. Since all the signs are positive, the only possible factorization of 2 is (2)( 1) and the only possible factorization of 5 is (5)(1). We have:
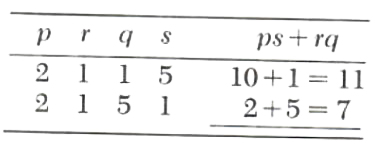
Thus,
2x^2+7x+5
=(px+q)(rx+s)
=(2x+5)(x+1)
Example 2. Factor 5y^2+13y-6.
Suppose 5y^2+13y-6=(py+q)(ry+s). The possible factorizations are tabulated below.

Thus,
5y^2+13y-6=(5y-2)(y+3)
Example 3. Factor 8a^2+22ab+15b^2.
Suppose 8a^2+22ab+15b^2=(pa+qb)(ra+sb). The possible factorizations are tabulated below.
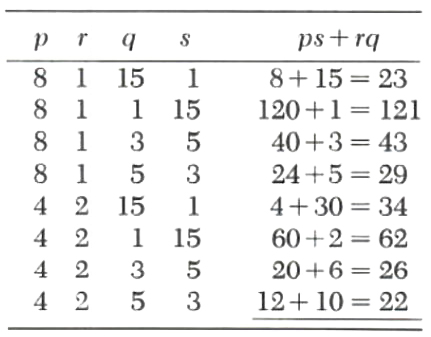
Therefore,
8a^2+22ab+15b^2=(4a+5b)(2a+3b)
Through practice, the student will learn to discard certain combinations mentally and this will cut clown on the number of combinations that he must try.
Certain polynomials provide us with clues as to which combinations we should try.
Example 4. Factor 2x^2+xy-3y^2-8x-12y.
Here we group the second degree terms and the first degree terms to obtain
2x^2+xy-3y^2-8x-12y
=(2x^2+xy-3y^2)-4(2x+3y)
In order for the polynomial to factor, we look for 2x^2+xy-3y^2 to have (2x + 3y) as one of its factors. We obtain
2x^2+xy-3y^2=(2x+3y)(x-y)
Hence,
2x^2+xy-3y^2-8x-12y
=(2x+3y)(x-y)-4(2x+3y)
=(2x+3y)(x-y-4)
Notice that this eliminates the need for a table since there is only one possibility that we need try.
3.6 The Sum and Difference of Two Cubes
We observe that
(a-b)(a^2+ab+b^2)
=a^3+a^2b+ab^2-ba^2-ab^2-b^3
=a^3-b^3
and
(a+b)(a^2-ab+b^2)
=a^3-a^2b+ab^2+ba^2-ab^2+b^3
a^3+b^3
Thus, a^3-b^3 and a^3+b^3 can be factored by the above equations.
Example 1. Factor x^3+27
x^3+27
=x^3+(3)^3
=(x+3)(x^2-3x+9)
Example 2. Factor 2x^8-16x^2.
2x^8-16x^2
=2x^2(x^6-8)
=2x^2[(x^2)^3-2^3
=2x^2(x^2-2)(x^4+2x^2+4)
Example 3. Factor (a-b)^3-(a+b)^3.
It is sometimes helpful to make the following type of substitution. Let
A=(a-b) and B=(a+b); then
(a-b)^3-(a+b)^3=A^3-B^3
=(A-B)(A^2+AB+B^2)
=[(a-b)-(a+b)[(a-b)^2+(a-b)(a+b)+(a+b)^2
=(a-b-a-b)(a^2-2ab+b^2+a^2-b^2+a^2+2ab+b^2)
=(-2b)(3a^2+b^2)
Example 4. Factor u^6-64.
We first note that this polynomial can be expressed as either the difference of two cubes or as the difference of two squares, namely,
u^6-64=(u^2)^3-(4)^3
or
u^6-64=(u^3)^2-(8)^2
The computations are simpler if we first factor it as the difference of squares. Therefore,
u^6-64=(u^3)^2-(8)^2
=(u^3-8)(u^3+8)
Each of these factors can be factored as the sum or difference of the square. Therefore,
u^6-64
=(u^3-2^3)(u^3+2^3)
=(u-2)(u^2+2u+4)(u+2)(u^2-2u+4)
3.7 Polynomials Which Can Be Made the Difference of Two Squares
Sometimes the simple device of adding and subtracting the square of a monomial can be used to transform a certain type of polynomial, which appears to be nonenforceable, into one that can be written as the difference of two squares.
First we notice that
(x^2+a)^2=x^4+2ax^2+a^2
Thus, a given polynomial, x^4+bx^2+a^2, will form a perfect square if and only if b = 2a. Now we apply this idea to some examples.
Example 1. Factor x^4+x^2+1
This does not factor by previous methods. Since a=1 we need a coefficient of 2 for x^2 in order to have a perfect square. Thus we add and subtract x^2 to obtain
x^4+x^2+1
=x^4+2x^2+1-x^2
=(x^4+2x^3+1)-x^2
=(x^2+1)^2-x^2
The last expression now factors as the difference of two squares. Therefore,
x^4+x^2+1
=(x^2+1)^2-x^2
=[(x^2+1)-x][(x^2+1)+x
=(x^2-x+1)(x^2+x+1)
Both of these factors are prime polynomials, so our factorization is complete.
Example 2. Factor 9m^4+8m^2+4
The polynomial does not factor by previous methods. Since 9m^4 and 4 are perfect squares, a middle term of 12m^2 would make the polynomial a perfect square. Thus,
9m^4+8m^2+4
=9m^4+12m^2+4-4m^2
=(3m^2+2)^2-(2m)^2
=[(3m^2+2)-2m][(3m^2+2)+2m
=(3m^2-2m+2)(3m^2+2m+2)
We observe that these two polynomials are prime so that the factorization is complete.
Example 3. Factor 4x^4-37x^2+9.
Since 4x^4 and 9 are perfect squares, a middle term of -12x^2 would make the trinomial a perfect square. Therefore,
4x^4-37x^2+9
=(4x^4-12x^2+9)-25x^2
=(2x^2-3)^2-(5x)^2
=(2x^2-5x-3)(2x^2+5x-3)
These polynomials factor, giving us
4x^4-37x^2+9
=(2x^2-5x-3)(2x^2+5x-3)
=(2x+1)(x-3)(2x-1)(x+3)
Notice that the original polynomial also factors by the method of Section 3.7, which yields
4x^4-37x^2+9
=(4x^2-1)(x^2-9)
=(2x-1)(2x+1)(x-3)(x+3)
Let’s see how our math solver factorizes this and similar problems. Click on "Solve Similar" button to see more examples.