Inequalities
Inequalities
9.1 Basic Properties
From Chapter 1 we recall that the real numbers are considered geometrically by looking at the real number line. The set of real numbers is the union of the three disjoint sets:
P : the positive real numbers
N: the negative real numbers
{0}: the set with t.he single element zero
![]()
Moreover, each real number a is either positive or 0, or -a is positive, and multiplication and addition obey the following rules of calculation:
(positive) ⋅ (positive) = (positive)
(negative) ⋅ (negative) = (positive)
(positive) ⋅ (negative) = (negative)
(negative) ⋅ (positive) = (negative)
(positive) + (positive) = (positive)
(negative) + (negative) = (negative)
The ordering relation less than in the real number system is defined by using the set of positive real numbers. Let a and b be any real numbers.
a is less than b, denoted by (a)<(b), if and only if b-a is positive
Three other order relations are
a is less than or equal to b, denoted by a<=b, if and only if (a)<(b) or a=b
a is greater than b, denoted by a>b, if and only if (b)<(a)
a is greater than or equal to b, denoted by a>=b, if (b)<(a) or b=a
Sometimes we want to emphasize that the order relation of a to b is < rather than ≤ , in which case we say that a is strictly less than b.
Any statement using one of the four order relations is called an inequality. There are five basic rules used in computations with inequalities.
I.1 If a and b are any real numbers, then exactly one of the following
is true:
(a)<(b), a=b, (b)<(a)
I.2 If (a)<(b) and (b)<(c), then (a)<(c).
I.3 If (a)<(b) and c is any real number, then a+c=b+c.
I.4 If (a)<(b) and c>0, then (ac)<(bc).
I.5 If (a)<(b) and (c)<0, then ac>bc.
In our computations, rules I.3, I.4, and I.5 are the most useful ones.
In more advanced courses one proves that rules I.1 through I.5 are true for real numbers by using the definition of < and the properties of P, N. and {0} listed above. For those who are interested we include, as a sample, a proof of 1.2.
If (a) < (b) and (b) < (c), then from the definition, b-a is positive and c-b is positive. By the property of P that (positive)+(positive) = (positive), it follows that (c- b) + (b - a) is positive. But
(c-b)+(b-a)=c-b+b-a=c-a
Thus c — a is positive, so by the definition, (a) < (c).
Using the real number line we see that (a) < (b) if and only if a is to the left of b. The other order relations have similar interpretations. Using the geometric interpretation of < we can interpret the five basic rules.
I.1 If a and b are points on the real number line, then exactly one of
the following is true:
a is to the left of b, a = b, b is to the left of a
I.2 If a is to the left of b and b is to the left of c, then a is to the left of c
I.3 If a is to the left of b and c is any real number, then a+c is to the left of b+c.
I.4 If a is to the left of b and c is greater than 0, then ac is to the left of bc.
I.5 If a is to the left of b and c is less than 0, then be is to the left of ac.
In Chapters 6 and 7 we considered methods of solving equations in one or more variables. In this chapter we will consider methods for solving inequalities in one or two variables. By the solution set of an inequality in one variable, we mean all those real numbers that satisfy the inequality. Frequently such solution sets will be unions of segments and half lines on the real number line. Some notational conventions are illustrated below:
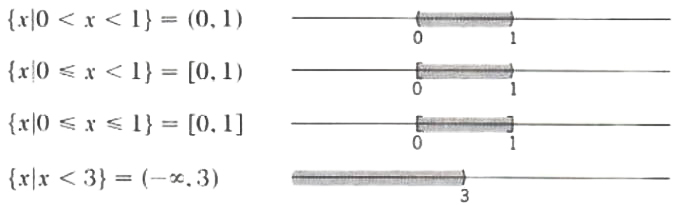
The first three subsets of the line are intervals, and the fourth is a half line, or ray.
The solution set of an inequality in two variables is the set of all numbers pairs that satisfy the inequality. Its graph is a region of the coordinate plane.
Two inequalities having the same solution set are equivalent. As with equations, the solution of a given inequality is obtained by fending an equivalent inequality whose solution set is known.
We conclude this section with some examples involving inequality relations.
Example 1. Which of the following are true? (a) -1/2<-3/7, (b) 3.2>=17/5.
(a) Computer -3/7-(-1/2).
-3/7-(-1/2)
=-3/7+1/2
=-6/14+7/14
=1/14
Since -3/7-(-1/2)=1/14is positive, the inequality is true.
(b) Compute 3.2-17/5.
3.2-17/5
=32/10-17/5
=16/5-17/5
=-1/5
Since 3.2-17/5=-1/5 is negative, the inequality is false.
Example 2. Graph each of the following and write in interval notation,
(a) ![]()
(b) ![]()
(c) ![]()
(a)
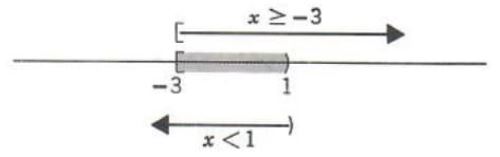
![]()
=(-3+∞) {intersect} (-∞,1)
=(-3,1)
(b)
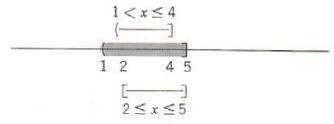
![]()
=(1,4) {union} [2,5
=(1,5)
Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
(c)
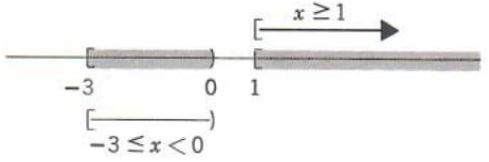
![]()
=(1,+∞) {union} (-3,0)
From the graph we see that no further simplification is possible
9.2 Linear Inequalities in One Variable
We can use the properties of inequalities that we listed in the previous section to solve linear inequalities in one variable, that is, any inequality that can be transformed by elementary operations to one of the following forms.
ax+b<0
ax+b<=0
ax+b>0
ax+b>=0
Example 1. Solve the inequality
4x-3>=2x+5
Add -2x to both sides (I.3)
2x-3>=5
Add 3 to both sides (I.3)
2x>=8
Multiply both sides by 1/2 (I.4)
x>=4
The solution set is therefore
![]()
= (4,+∞)
This is represented geometrically by
![]()
Example 2. Solve the inequality
(2x+1)/(-3)<=2
Multiply by -3
2x+1>=-6
Note that multiplication by a negative number reverses the inequality.
Add -1 to both sides, then multiply by 1/2. (I.3,I.4)
x>=-7/2
The solution set is therefore
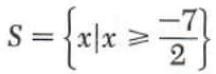
=(-7/2,+∞)
This is illustrated geometrically by

Example 3. Solve the inequality
-3<3x-2<=7
This inequality means that x must satisfy the system of inequalities
-2<3x-2
3x-2<=7
However, we may solve both inequalities simultaneously.
-2<3x-2<=7
Add 2 to all three expressions
0<3x<=9
Multiply all three expressions by 1/3.
0<(x)<=3
The solution set is therefore
![]()
=(0,3)
This is represented geometrically by
![]()
Example 4. Solve the inequality
-8<=2-3x<6
Add -2 to all three expressions.
-10<=-3x<4
Multiply by -1 /3, changing the direction of both inequalities.
10/3>=x>-4/3
The solution set is therefore
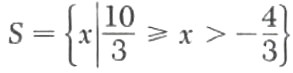
=(-4/3,10/3)
This is represented geometrically by

Let’s see how our inequality solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
9.3 Inequalities Involving Absolute Values
Recall from Chapter 1 that the distance between x and a on the real number line is |x-a|. If x, a, and b are real numbers and |x- a| < (b), then x must be at a distance less than b from a. This is represented geometrically in Figure 1.

Figure 1
We see that the inequality
|x- a| < (b)
has as its solution set
![]()
=(a-b,a+b)
Similarly if x satisfies the inequality
|x- a| < (b)
then x must be at a distance greater than b from a. This is represented in Figure 2.
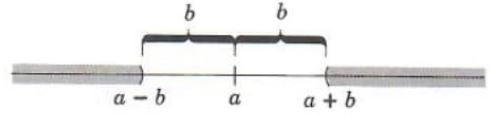
Figure 2.
We see that the inequality |x- a| < (b) has as its solution set
![]()
=(-∞,a-b) {union} (a+b,+∞)
Example 1. Solve the inequality
|x-1/2|<5
Graphing we have

The solution set is
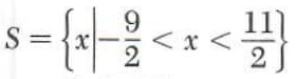
=(-9/2,11/2)
Example 2. Solve the inequality
|x-2|>3
Graphing we have
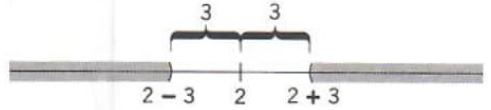
The solution set is
![]()
=(-∞,-1) {union} (5,+∞)
Example 3. Solve the inequality
|x+1|<=3
First note that
|x+1|=|x-(-1)|
so that |x+1| is the distance from x to -1
Graphing we have

Since the relation is ≤ , the end points are included in the solution set, which is
![]()
=-4,2
Example 4. Solve the inequality
|4-x|>5
Note that |4-x| is the distance between 4 and x, which is the same as the distance between x and 4, namely, |x-4|. Thus the above inequality is equivalent to the inequality
|x-4|>5
whose graph is
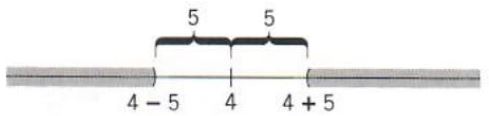
The solution set is
![]()
=(-∞,-1) {union} (9,+∞)
Since |u| = |u-0|, which is the distance from u to 0, the inequality
|u|<(a)
is equivalent to
|u-0|<(a)
which is equivalent to
(-a)<(u)<(a)
If u=ax+b, we see that
|ax+b|<(c)
is equivalent to
(-c)<(ax+b)<(c)
which can be solved as in the preceding section. Similarly
|ax+b|>(c)
is equivalent to
![]()
Example 5. Solve the inequality
|2x-3|<4
This inequality is equivalent to
-4<2x-3<4
We add 3 and then multiply by 1/2.
-1<(2x)<7
-1/2<(x)<7/2
The solution set is
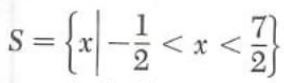
=(-1/2,7/2)
Let’s see how our inequality solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
Example 6. Express -1<(x)<5 in the form |x-a|<(b).
The graph of -1<(x)<5 is
![]()
The midpoint of this interval is
(5+(-1))/(2)=2
which is at a distance 3 from the end points -1 and 5. Thus x must be a. distance less than 3 from the midpoint 2, which gives us
|x-2|<3

9.4 Nonlinear Inequalities in One Variable
By a quadratic inequality in one variable, we mean an inequality of any of the following forms.
ax^2+2x+c<0
ax^2+2x+c<=0
ax^2+2x+c>0
ax^2+2x+c>=0
where a!=0. Any inequality that can be transformed by means of our elementary operations to an inequality of the above type can of course be treated by the same methods.
We will use the following properties of real numbers.
R.1 If AB<0, then there are two cases:
(a) A<0 and B>0
(b) A>0 and B<0
R.2 If AB>0, then there are two cases:
(a) A>0 and B>0
(b) A<0 and B<0
In the case R.1, A and B must have opposite sign, while in the case R.2, A and B must have the same sign.
Example 1. Solve the inequality
2x^2+5x-3>0
We first factor to obtain
(2x-1)(x+3)>0
From R.2 there are two cases:
(a) 2x-1>0 and x+3>0
(b) 2x-1<0 and x+3<0
Since a number x is a solution of the original inequality if and only if it satisfies either (a) or (b), the complete solution set of the original inequality is the union of the solution set of (a) with the solution set of (b).
(a) 2x-1>0 and x+3>0
Therefore
2x-1>0 and x+3>0
2x>1 and x>-3
x>1/2 and x>-3
Since x must satisfy both conditions, the solution set for (a) is
![]()
= ![]()
= (1/2,+∞)
Geometrically,

(b) 2x-1<0and x+3<0
Therefore,
2x-1<0 and x+3<0
2x<1 and x<-3
x<1/2 and x<-3
The solution set for (b) is
![]()
= ![]()
=(-∞,-3)
Geometrically,

Recall that the solution set of the original equation is the union of the sets obtained in parts (b) and (a), namely,
S=S_b {union} S_a
=(-∞,-3) {union} (12,+∞)
Geometrically,

Another method for solving a quadratic inequality is to indicate on a number line where each factor is positive, negative, or zero. Applying this method to Example 1 we have
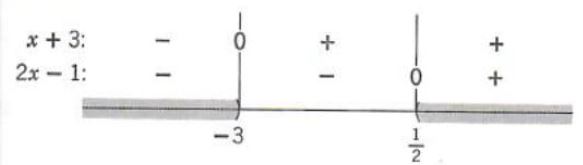
Since the product (x+3)(2x-1) is to be positive, the solution set is given by the regions where both factors have the same sign. From the diagram we see that this is S = (-∞, -3) {union} (1/2,+∞)
This method is easier to use than the first method, especially if there are more than two linear factors.
Example 2. Solve the inequality
(x-2)(x+1)(x-1)<=0
Since the product of the three factors is to be non-positive, the solution set will be those numbers for which at least one of the factors is zero or an odd number of the factors is negative.
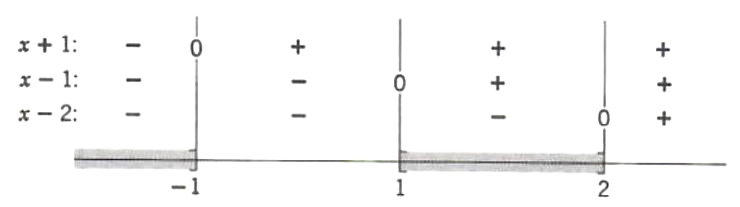
Thus the solution set is
S=(-∞,-1) {union} [1,2
This method also applies to a rational expression whose numerator and denominator can be factored into linear factors.
Example 3. Solve the inequality
(x-1)/(x+2)<=2
We first transform this inequality to an equivalent inequality that has zero on the right-hand side.
(x-1)/(x+2)-2<=2
(x-1-2(x+2))/(x+2)<=0
(-x-5)/(x+2)<=0
As before,
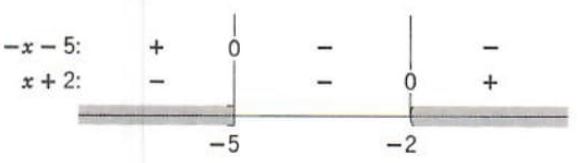
Note that -2 is excluded since the denominator is zero there. The solution set is
S=(-∞,-5) {union} (-2,+∞)
Let’s see how our inequality solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
9.5 Linear Inequalities in Two Variables
An inequality of any of the forms
ax+by+c<0
ax+by+c<=0
ax+by+c>0
ax+by+c>=0
with a and b not both zero is called a linear inequality in two variables.
The solution set of such an inequality is one of the two half-planes determined by the line ax+ by + c = 0.
2x-y+2<0
First graph 2x-y+2=0

To see that the solution set is, in fact, one of the half-planes of the line, we solve the inequality for y obtaining
y>2x+2
The points (x,y) satisfying y>2x+2 are those that are above the points on the line y = 2x +2, namely, the points in the half-plane above the line. Since the inequality is strict the points on the line are not in the solution set. We indicate this with a dotted line.
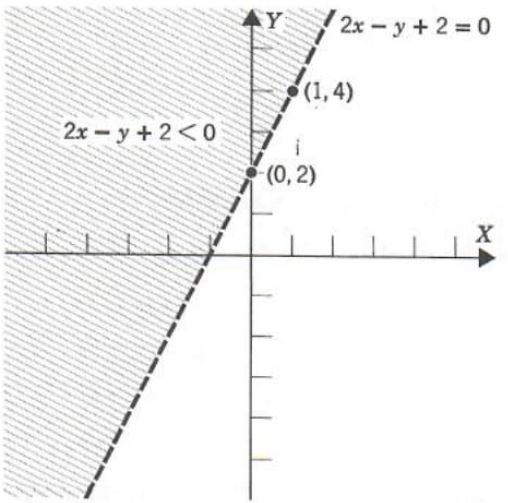
Algebraically the solution set is
![]()
Example 2. Solve the inequality
x-3y+2>=0
Solve the inequality for x obtaining
x>=3y-2
Since x is greater to the right, the solution set is the half-plane to the right of the line x-3y+2=0. Since the inequality is not strict, points of the line are included in the solution set. We first graph the line and then shade in the half-plane.
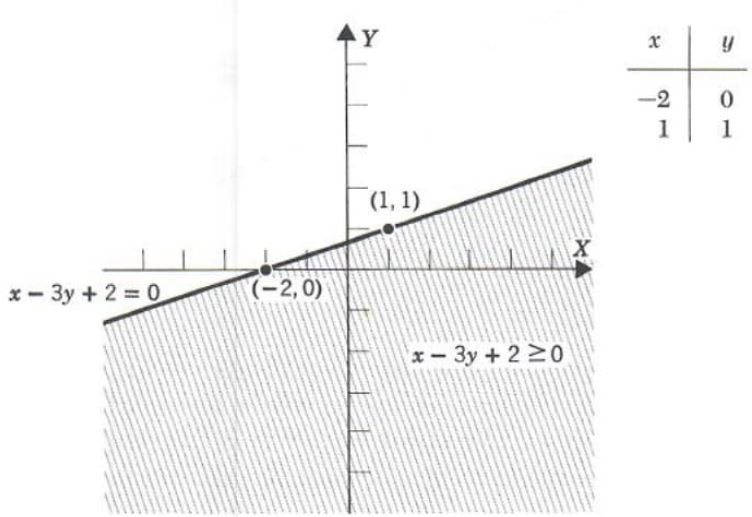
An alternate method for discovering the solution half-plane is to substitute the coordinates of a point not on the line into the inequality. If the inequality is satisfied, the solution set is the half-plane including this point, and the other half-plane otherwise. The point (0,0) is easy to use if it is not on the line. In Example 2, substituting (0,0) we obtain
x-3y+2>0
(0)-3(0)+2>0
2>0
Since (0,0) satisfies the inequality the solution set is the half-plane containing (0,0).
Systems of inequalities may be handled in a similar manner. We obtain the solution set graphically by finding the intersection of the solution half-planes of the individual inequalities in the system.
Example 3. Solve the inequality
(1) y-2x+3>0
(2) 2y+x-1<=0
Graph the corresponding lines l_1l_2:
l_1 y-2x+3=0
l_2 2y+x-1=0
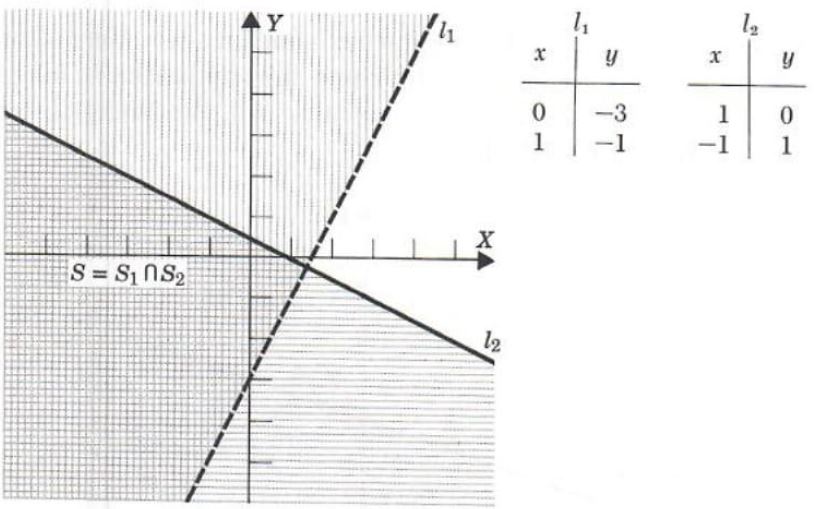
By one or the other of the above methods we find that the solution set S_1, of (1) is the half-plane above l_1, while the solution set S_2 of (2) is the half-plane below l_2 The solution set S_1 is illustrated by vertical lines, while S_2 is illustrated by horizontal lines. Hence, the solution set S of the system is
S=S_1 {intersect} S_2
= ![]()
which is the region where the horizontal and vertical lines overlap.
Example 4. Solve the system
(1) x-y+1>=0
(2) x<1
(3) y>=-3
Consider the following equations.
l_1: x-y+1=0
l_2: x=1
l_3: y=-3
We find that the solution set S_1, of (1) is the half-plane below l_1, the solution set S_2 of (2) is the half-plane to the left of l_2, and the solution set S_3 of (3) is the half-plane above la. The solution set is
S=S_1 {intersect} S_2 {intersect} S_3
= ![]()
which is illustrated in Figure 3
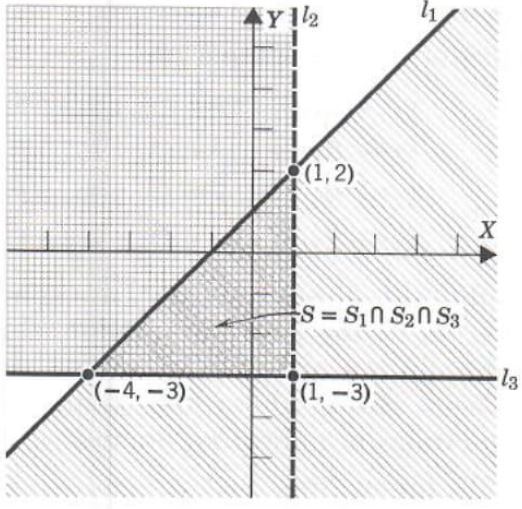
Figure 3
9.6 Quadratic Inequalities in Two Variables
An inequality of any one of the forms
Ax^2+Bxy+Cy^2+Dx+{Epsilon}y+F<0
Ax^2+Bxy+Cy^2+Dx+{Epsilon}y+F<=0
Ax^2+Bxy+Cy^2+Dx+{Epsilon}y+F>0
Ax^2+Bxy+Cy^2+Dx+{Epsilon}y+F>=0
with A, B, and C not all zero, is called a second degree inequality in two variables. As in the previous section, the solution is best described graphically as a certain subset of the plane. We will only consider the special cases where the graphs of the corresponding equalities are circles or parabolas, as studied in Chapter 7.
Example 1. Solve the inequality
-x^2+y+6x-10<=0
Graph the equation
-x^2+y+6x-10=0
Complete the square
y=x^2-6x+10
y-1=(x-3)^2
We see that the vertex is at (3, 1) and the parabola opens up. We plot a few points to draw the graph. (See Figure 4.) Since y <= x^2-6x+ 10 we have as our solution set all points (x, y) in the plane below and on the parabola. The solution set is described algebraically as
![]()
Example 2. Solve the inequality
x^2-4x>=-y^2-2y+4
Graph the equation
x^2-4x=-y^2-2y+4
Complete the square.
x^2-4x+4+y^2+2y+1=4+4+1
(x-2)^2+(y+1)^2=3^2
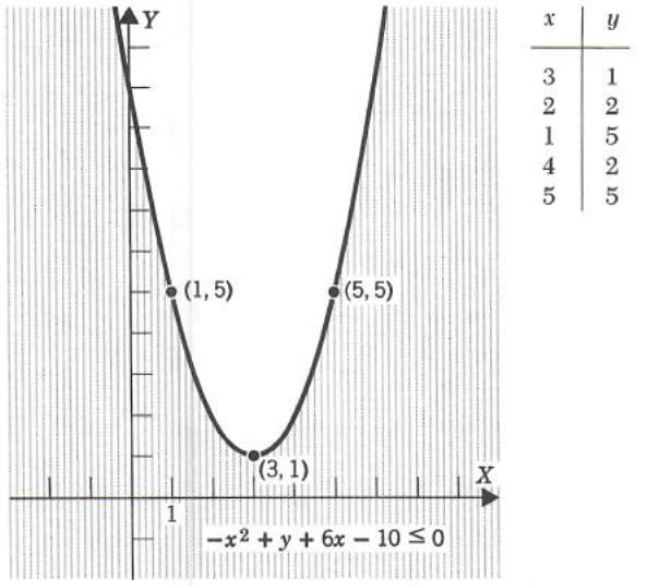
FIGURE 4.
From Chapter 7 we recall that this equation has as its graph a circle of radius 3 with center at (2, -1). (See Figure 5.) Since the original inequality is
x^2-4x>=-y^2-2y+4
which is equivalent to
(x-2)^2+(y+1)^2>=3^2
our solution set S is the set of all points outside and on the circle. Thus,
![]()
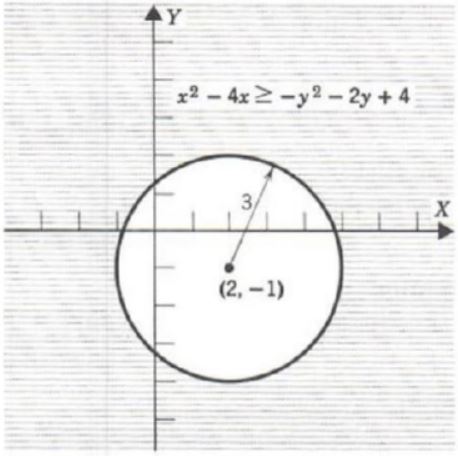
FIGURE 5.
Let’s see how our inequality solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
Example 3. Solve the inequality
2x-3y+6>=0
y>=x^2-2x-3
Graph the straight line
l: 2x-3y+6=0
Graph the parabola
p: y=x^2-2x-3
=(x-1)^2-4
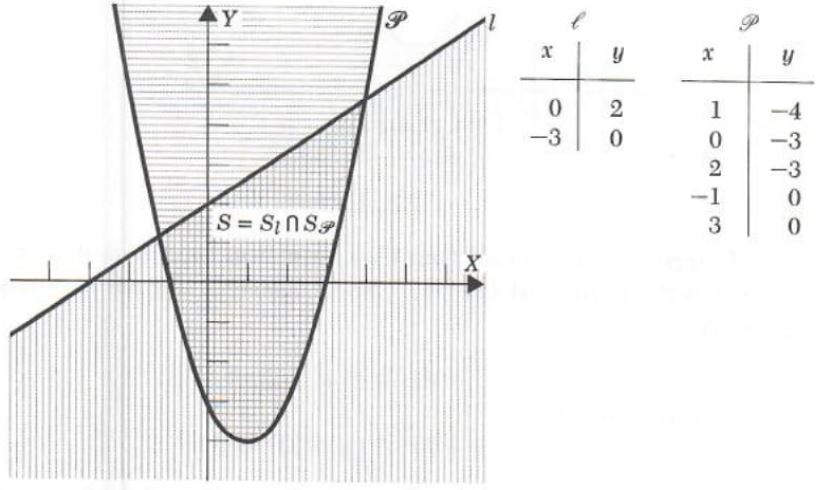
Since the point (0,0) satisfies both inequalities, the solution set S is the intersection of the half-plane S_l below the line and the region S_p above the parabola. Thus
S=S_l {intersect} S_p
= ![]()
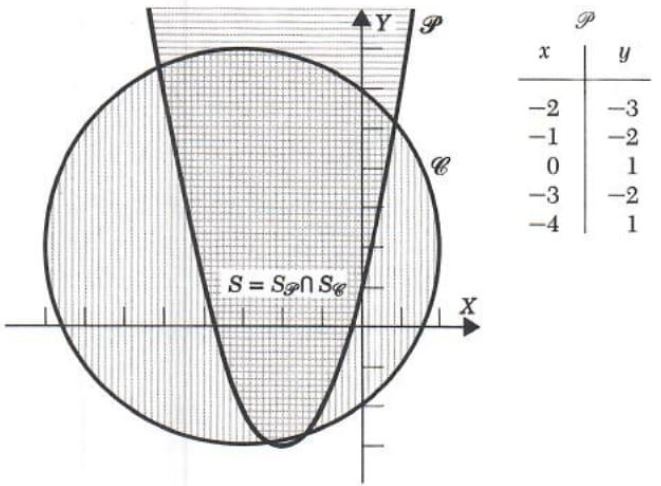
Example 4. Solve the inequality
y-x^2>=4x+1
x^2+y^2<12+4y-6x
Graph the parabola
p: y=x^2+4x+1
y+3=(x+2)^2
Graph the circle.
l: x^2+6x+y^2-4y=12
(x+3)^2+(y-2)^2=5^2
The parabola p has vertex at (-2,-3) and opens up, while the circle l has center at (-3, 2) and radius 5. The original system of inequalities is equivalent to the system
y>=(x+2)^2-3
(x+3)^2+(y-2)^2<=5^2
The solution set S_p is the set of all points above and on the parabola, while the solution set S_l is the set of all points inside and on the circle. Thus the solution set of the original system is
S=S_p {intersect} S_l