System of Equations
Operations on Sets
In order to better understand the concept of solving a system of equations, we will need to become familiar with some facts on sets.
If A and Bare sets, then we say that A is a subset of B if each element of A is also an element of B. We write A {subset} B. We sometimes say that is contained in B instead of A is a subset of B. For example,A{1, 2, 3} is a subset of B = {1, 2, 3, 4, 5} since each element of A is also an element of B, while C = {1, 2, 7} is not a subset of B since 7 is an element ofC, but not of B.
IfA and B are sets, then by the union of A and B, which we write A {union} B, we mean the set of all elements that are in A or in B or in both.
Example 1. If A = {2, 4, 6, 8, 10} and B = {3, 4, 5, 6, 7, 8, 9} find A {union} B.
A {union} B= {2,3,4,5,6,7,8,9, 10}
Even though 4, 6, and 8 are in both sets, they are listed only once in the union.
If A and B are sets, then by the intersection of A and B, which we denote by A {intersect} B, we mean the set of all elements that are in bothA and B
Example 2. If C = {2, 4, 6, 8} and D = {4, 5, 6, 7, 8} find C {intersect} D.C {intersect} D = {4, 6, 8} If S = {1, 2, 3}, and T= {5, 6, 7}, then S {intersect} T is the set with no elements, that is, the empty set {empty}). If the intersection of two sets is empty, that is, they have no elements in common, then we say that the two sets are disjoint. Thus S andT are disjoint.
When more than one set operation is to be performed, we use parentheses to indicate the order in which they are to be performed.
Example 3. If A = {1, 2, 3}, B = {2, 3, 4, 5, 6}, and C = {5, 6, 7, 8}, find(A {intersect} B) {union} C and (A {intersect} C) {union} B
Since
A {intersect} B = {2,3}
we have
(A {intersect} B) {union} C= {2,3} {union} {5,6,7,8}
{2, 3, 5, 6, 7, 8}
Also, since
A∩C={1,2,3}∩{5,6,7,8}={empty}
we have
(A∩C)∪B={empty} ∪{2,3,4,5,6}
={2,3,4,5,6}
=B
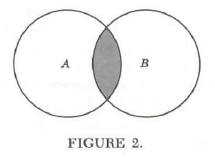
We may diagram the operations of union and intersection on sets by Venn diagrams.If the sets A andB are represented by circular regions, then the diagram ofA {union} B is the shaded area in Figure
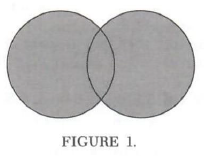
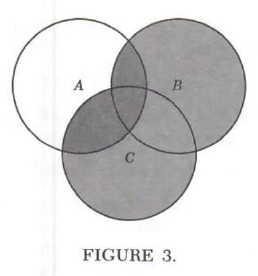
ofA {intersect} B is the shaded region in Figure 2. The diagram of the set A {intersect} (B {union} C) is the shaded region in Figure 3, which we find by first locating B {union} C and then shading what it has in common with A.
Another important set operation is the operation of set difference. If A and B are two sets, then A - B is the set of all elements of A that are not in B. The diagram of this set is given in Figure 4.
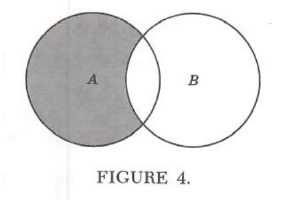
Example 4. If A = {1, 2, 3, 4, 5, 6, 7, 8} and B = {2, 4, 5, 7, 11, 13, 14} find A-B and B - A.
A-B ={1, 3, 6, 8}
B-A = {11, 13, 14}
We have described the sets in the examples above by listing the elements. This is not practical in many cases. Another way of describing a set is to state a property P(S) that is true for exactly those members X in the set. We denote the set Sdescribed by property P(S) by
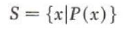
This notation is read:
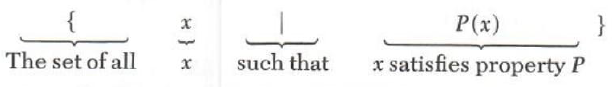
For example, let E be the set of positive even integers. A property P(n) that is true for exactly these integers is “n is an integer, n > 0, and n is divisible by2.” Using the notation above we have 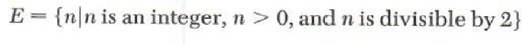
If T is a set of pairs of numbers and the describing property is Q(x, y), then we write
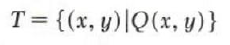
For example, the setCof all points in the plane on the circle whose radius is 2and whose center is at the origin is

The study of sets and operations on sets is itself a fascinating subject, but our purpose here is simply to introduce the subject to the student so that he may apply it to the study of the solution of systems of equations and, in Chapter 9, to the solution of systems of inequalities.
8.2 Graphical Solution
Consider the system of two linear equations in two variables x and y.
(1) a_1x+b_1y+c_1 =0 (a_1, b_1 not both 0)
a_2 x+b_2 y+c_2=0 (a_2, b_2 not both 0)
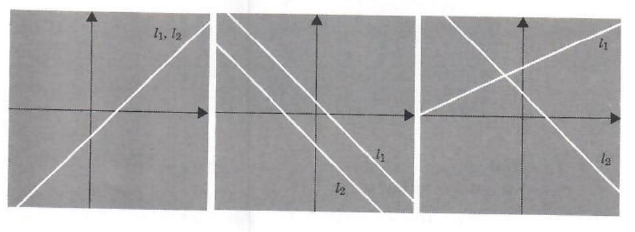
Since the graph of each equation is a straight line we have the following three possibilities.
(a) The graphs are the same straight line.
(b) The graphs are parallel distinct lines.
(0) The graphs intersect in exactly one point.
Graphically:
If we denote the solution sets of the equations in (1) by
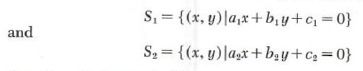
then the solution set S of (1) is
S=S_1 {intersect} S_2
From above, we see that in case (a)S=S_1=S_2 in (b) S={empty}, while in (c) Swould consist of a single point (p, q). In case (a) the system is said to be dependent, in case (b) the system is said to be inconsistent, and in case (c) the system is said to be independent.
In Chapter 7 we pointed out that there is exactly one line through a given point having a given slope. A consequence of this is that two distinct nonvertical lines are parallel if and only if they have the same slope.
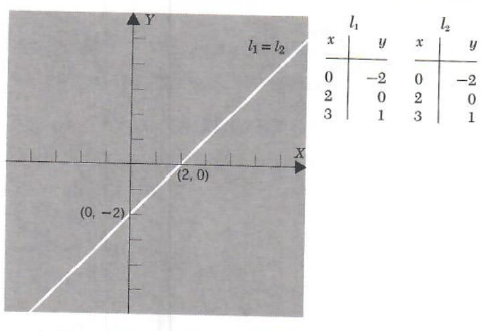
Example 1. Solve the system and classify.
2x + y = 4
x-y=2
Graphing the two equations we have
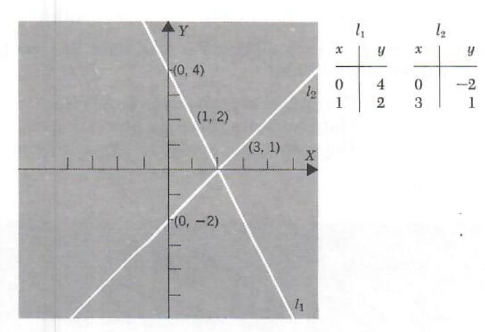
We see that the point of intersection appears to be (2, 0). If this is the case, then the solution set is
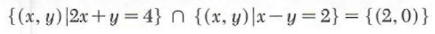
Since the solution set consists of a single point, the system is consistent. Note that graphical solutions are approximations.
Example 2. Solve the following system and classify.
x-y=2
-(1/2)x+1/2y=-1
Graphing the two equations we have
We see that the two equations have the same straight line for their graph and hence the solution set is
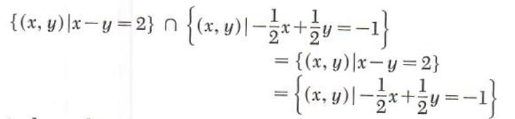
The system is dependent.
Example 3. Graph the system and classify.
y -2x = 4
2x - y = 2
Graphing the two equations we have
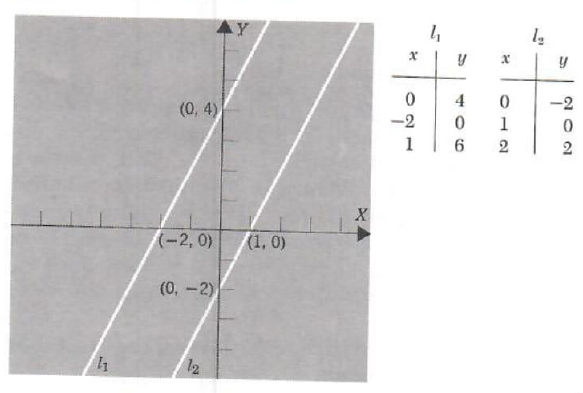
We see that the slope of each line is 2, so the lines are parallel, and therefore the system is inconsistent. The system has as its solution set
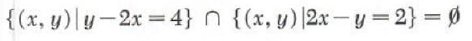
Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
8.3 Solution by Substitution
In general, the solution of a pair of linear equations in two variables can only be approximated by looking at their graphs. In order to find the exact solution set we transform the given system to one whose solution set is readily obtainable. We must make sure that the solution sets of the original system and the resulting system are the same. Two systems having the same solution set are said to be equivalent. Certainly if we obtain a new system by replacing one equation in the old system by an equivalent equation, then the two systems are equivalent.
The method we present here for finding the exact solutx = 1 -2yion is called the method of substitution.
Consider the general system
(1) a_1x+b_1y=c_1
a_2x+b_2y=c_2
As before, we assume that at least one of the coefficients a_1,a_2,b_1,b_2 is different from zero. If b_1!=0, we solve the first equation for y, obtaining the equivalent equation
y=-(a_1/b_1)x+c_1+b_1
Thus, the system (1) is equivalent to
(2) y=-(a_1/b_1)x+c_1/b_1
a_2x+b_2y=c_2
If (x,y) is a solution of (2), then y is given in terms of x by the first equation. Substituting this expression in the second equation we obtain the equivalent system
y=-(a_1/b_1)x+c_1/b_1
a_2x+b_2(-(a_1/b_1)x+c_1/b_1)=c_2
The second equation may be solved for x and the corresponding value of y can be obtained from the first equation. The other cases are handled in a similar manner.
Example 1. Solve the system
2x-y=4
x-y=2
Solve the first equation for y to obtain
y = -2x +4
The system
y = -2x +4
x-y=2
is equivalent to the original system.
Substituting, we obtain the equivalent system
y = -2x +4
x-(-2x+4)=2
or
y = -2x +4
x = 2
Substituting, we obtain
y = -2 (2) +4
=0
The solution set is therefore
S = {(2, 0)}
Example 2. Solve the system
2x - y = 3
4x -2y = 6
Solve the first equation for y obtaining the equivalent system
y = 2x -3
4x - 2y = 6
Substituting, we obtain
y = 2x -3
4x-2(2x-3) = 6
or
y = 2x -3
6 = 6
Since the second equation is satisfied for all (x, y), this system has as its solution set
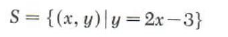
Therefore the original system is dependent.
Example 3. Solve the system
x +2y = 3
x = 1-2y
Since the second equation is solved forx we substitute in the first equation obtaining
(1 -2y) +2y = 3
x=1-2y
or
1 = 3
x=1-2y
Since the first equation has as its solution set {empty}, the solution set of the system is
S ={empty}
The original system is therefore inconsistent.
Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
8.4 Solution by Elimination
The method of solution by elimination depends on the elementary operations E1, E2, and E3 below, which change a given system into an equivalent system.
E.1 Interchange any two equations of the system.
E.2 Multiply any equation by a nonzero number.
E.3 Replace any equation of the system by the sum of that equation and a multiple of another equation of the system.
Example 1. Solve the system
x+y=4
2x - 3y= 3
Applying E.3 we multiply the first equation by -2 and add it to the second equation obtaining the system
x+y=4
-5y = -5
Apply E.2 to the second equation by multiplying by -1/5.
x+y=4
y = 1
Substituting, we obtain
x+1=4
y = 1
or
x = 3
y = 1
Thus the solution set of the original system is
S = {(3, 1)}
Example 2. Solve the system.
x + 2y = 3
2x +4y = 1
Add -2 times the first equation to the second equation to obtain the system
x + 2y = 3
0= -5
Since the second equation obviously has no solution, this system, and hence the original system, is inconsistent. Thus the solution set is
S ={empty}
Example 3. Solve the system
2x - y = 3
-x+1/2y=-(3/2)
Multiply the first equation by 1/2 and add it to the second equation to obtain the system
2x - y = 3
0=0
Since the second equation is satisfied for all (x, y), the solution set of system is the same as the solution set of the first equation, namely,
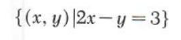
The original system is dependent.
We conclude this section with two examples of systems that lead to systems of linear equations.
Example 4. Solve the system
(1) x-y)/(x+y)=2/3
(x+2y)/(x-3)=1/2
Multiply each equation by its LCD.
(2) 3x-3y = 2x+2y
2x + 4y = x - 3
Simplify.
x -5y = 0
x +4y = -3
Multiply the first equation by -1 and add.
x -5y = 0
9y = -3
Substituting, we obtain (5/3, -1/3) as the solution of (2). In going from (1) to (2) we multiplied by the expressions x + y and x -3. Multiplication by each of these expressions is an elementary operation only if the expression is non-zero. By substitution we see that neither expression is zero at (5/3, -1/3).
Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.
Example 5. Solve the system
(1) 1/(x-y)+2/(x+y)=7/10
4/(x-y)+5/(x+y)=5/2
Multiplication of each equation by its L.C.D. leads to nonlinear equations. However, we notice that the two variables xand y occur only in the combinations 1/(x - y) and 1/(x + y), so that the substitutions
a=1/(x-y) and b=1/(x+y)
8.5 Solution by Determinants
In solving the system
(1) a_1x+b_1y = c_1
a_2x+b_2y = c_2
we encounter the expression
a_1b_2-a_2b_1
This expression is denoted by
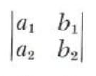
and is called the determinant of a_1,b_1,a_2,b_2. Since this determinant has two rows and two columns, it is said to be of order 2. The numbers a_1,b_1,a_2 and b_2 are called the elements of the determinant.
For example,
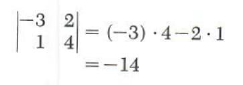
We will now show how determinants can be used to solve the system (1) above.
a_1x+b_1y = c_1
a_2x+b_2y = c_2
Multiply the first equation by , the second equation by -b_1, and add to obtain
a_1b_2x-a_2b_1x=c_1b_2-c_2b_1
a_2x+b_2y=c_2
Solving the first equation for x, we obtain
x=(c_1b_2-c_2b_1)/(a_1b_2-a_2b_1
We see that the numerator is simply the determinant
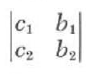
while the denominator is the determinant
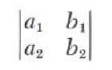
Hence, we may write
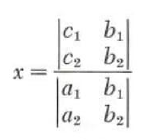
where we are assuming, of course, that
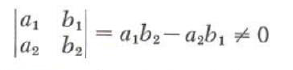
Solving the original system for y instead of x, we obtain
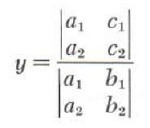
Let D, D_x, and D_y denote the following determinants:
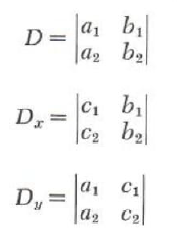
Using this notation, the solutions forx andy above become
x=D_x/D
y=D_y/D
The use of determinants in this way to solve a system of linear equations is known as Cramer’s rule.Gabriel Cramer (1704-1752) was a well-known Swiss mathematician.
We see thatD is the array of coefficients ofx and y in (1). Further more, D_x is obtained from D by replacing the first column, the x coefficients, by the column of constants; and, similarly, D_y is obtained from D by replacing the second column, the y coefficients, by the column of constants.
Example 1. Use Cramer’s rule to solve the following system.
x-y=2
x+y=4
We compute D, D_x, and D_y.

Apply Cramer’s rule.
x=D_x/D
=6/2
=3
y=D_y/D
=2/2
=1
Thus the solution set is S = {(3, 1)}.
If D =0 in this procedure, then either the equations are dependent or the system is inconsistent, depending on whether D_x, and D_y are both zero or not.
Example 2. Solve the system
2x-4y=3
-x+2y=-(3/2)
We have
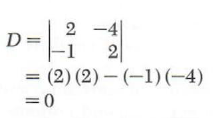
Consequently, the system is either dependent or inconsistent. Since
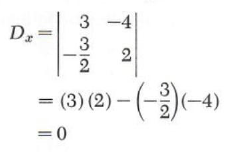
and
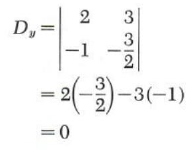
the system is dependent. From geometric considerations two equations are dependent if and only if they are equations of the same line.
Thus the solution set is
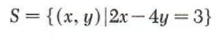
8.6 Linear Systems in More than Two Variables
Frequently we must consider systems of equations with more than two unknowns. The methods of substitution, elimination, and Cramer’s rule can be extended to solve these higher-order systems.
In this section we will use the method of elimination.
Example 1. Solve the system
x+y-4z=2
3x-y-8z=-1
2x+3y+2z=3
We eliminate x from the second equation by adding -3 times the first equation, and from the third equation by adding -2 times the first equation, obtaining the system
x+y-4z=2
-4y+4z=-7
y+10z=-1
Eliminate y from the second equation by adding 4times the third equation to the second obtaining the system
x+y-4z=2
44z=-11
y+10z=-1
We can use the last two equations to solve for two of the variables in terms of the third variable. Thus
x=23-11z
and
y=14-9z-2x
=14-9z-2(23-11z)
so
y=-32+13z
The solution set is
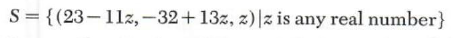
Sincez takes on all real values, S has an infinite number of elements.
Therefore the system is dependent.
Example 4. Solve the system
x+y+z=1
2x - 3y - 2z = -4
4x - y = -1
Eliminatingz in the second equation we obtain
x+y+z=1
4x - y = -2
4x - y = - 1
Eliminating y in the last equation we obtain
x+y+z=1
4x - y = -2
0=1
Since the last equation in this system has no solution, the system is inconsistent. Hence the original system is inconsistent and has solution set S={empty}.
8.7 Third-Order Determinants
By a determinant of order 3 we mean
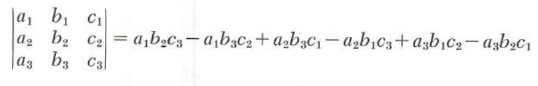
If we rewrite this number in the form
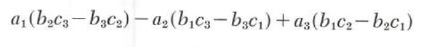
then we may rewrite it in terms of determinants of order 2 as follows.
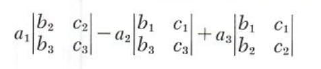
We may also rewrite it as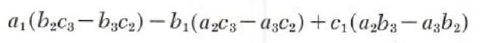
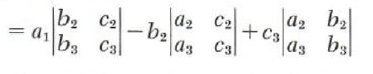
We define the minor of a given element in a determinant to be the determinant that is left after deleting the row and the column in which the element appears. Thus in the determinant of order 3
above, the minor ofa_1 is
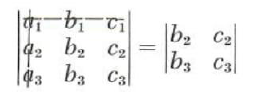
the minor of b_2 is
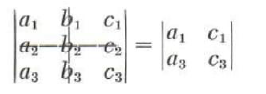
while the minor of c_3 is
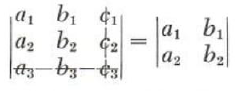
If we use the notation m(x) to stand for the minor of the element x, then from above, expanding by the first column, we have
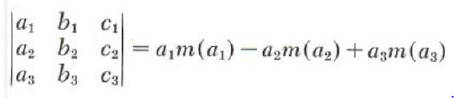
Expanding by the first row we have
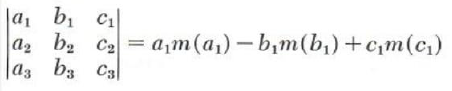
With the proper use of signs it is possible to express the determinant in terms of minors of any row or any column. A helpful device for determining the appropriate signs for a third-order determinant is the diagram below.
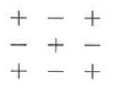
We can pick any row or column, form the sum of the product of the elements and their minors along with the appropriate sign from the diagram above, and we will have the determinant expressed in terms of minors.
Example 1. Use the second row to compute



We expand D by the first row to obtain
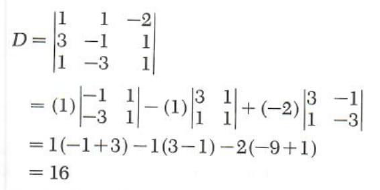
Expanding D_x I by the first column we have
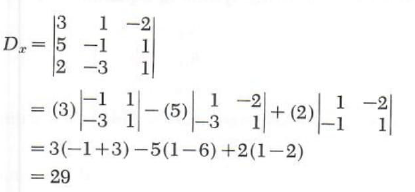
Similarly we find that
D_y=-5
and
D_z=-12
Hence,
x=D_x/D
=29/16
y=D_y/D
=-5/16
z=D_z/D
=-12/16
=-3/4
Therefore the solution set is S = {(29/ 16, -5/ 16, -3/4)
If D=0, then either the system is dependent or inconsistent, depending on whether D_x, D_y and D_z are all zero, or not.
8.8 Statement Problems
Many statement problems lead to systems of linear equations in two or more variables. The general method of attack is the same as in Section 6.6, except that we introduce a different letter for each unknown. Then we translate the statements relating these unknowns into a system of equations.
Example 1. A man has $2.00 in nickels and dimes, with two more dimes than nickels. How many dimes and how many nickels does he have?
Step 1. Let n be the number of nickels and d be the number of dimes.
Step 2. The value of n nickels is 5n cents and the value of d dimes is 10d. Since the man has $2.00 in nickels and dimes, we have the equation
5n+10d=200
Since he has two more dimes than nickels, we have
d=n+2
Step 3. Solve the system
5n+10d=200
d=n+2
By substitution
5n+10(n+2)=200
d=n+2
or
15n = 180
d=n+2
The solution is
n=12 nickels
d=14 dimes
Example 2. How many gallons of solution containing 45% alcohol must be mixed with a 60% alcohol solution to obtain 40 gallons of solution that is 48% alcohol?
Step 1. Let x be the number of gallons of 45% solution and y be the number of gallons of 60% solution.
Step 2. Since the total number of gallons is 40,
x+ y = 40
Since 45% of x is alcohol, 60% of y is alcohol, and 48% of the total 40 gallons is alcohol,
0.45x + 0.60y = (0.48) (40)
Step 3. Solve the system
x+ y = 40
45x + 60y = 1920
Adding -45 times the first equation to the second equation we obtain
x+ y = 40
15y=120
Thus,
y=8 gallons
x=32 gallons
Example 3. A man cruises 40 miles down a river in his boat in 2 hours. The return trip takes 2 1/2 hours. What is the average speed of the boat and the average speed of the river?
Step 1. Letx be the speed of the boat relative to the shore and y the speed of the river.
Step 2. Since distance is equal to rate times time and the boat’s speed downstream is x+ y, we have
40 = (x + y) (2)
Upstream we have
40 = (x - y) (5/2)
Step 3. Solve the system
x+ y=20
x-y=16
Adding the two equations we have
x+ y=20
2x=36
Thus,
x=18mph
y=2 mph
Example 4. A man paid for a $1.85 item with nickels, dimes, and quarters. If there were the same number of quarters as nickels plus dimes and four more nickels than dimes, how many of each were there?
Step 1. Let x be the number of nickels, y be the number of dimes, and z be the number of quarters.
Step 2. There were the same number of quarters as nickels plus dimes so
z=x+y
There were four more nickels than dimes so
x=y+4
The value of x nickels is 5x cents, of y dimes is 10y, and ofz quarters is 25z, thus
5x+10y+25z=185
Step 3. Solve the system
z=x+y
x=y+4
5x+10y+25z=185
Substituting forx in the first equation we obtain
z = (y +4) + y
x=y+4
5x+10y+25z=185
Now substituting for x and z in the third equation we obtain
z=2y+4
x=y+4
5(y +4) + 10y+ 25(2y+4) = 185
Solving this system we obtain
x=5 nickels
y=1 dime
z=6 quarters
8.9 Second Degree Systems in Two Variables
An equation of the form
(1) Ax^2+Bxy+Cy^2+Dx+Ey+F=0
where A, B, C, D, E, and F are all constants, is called the general second degree equation in x and y, or simply the general quadratic in x and y. In the case that A = B = C = 0 we see that (1) reduces to a first degree equation whose graph is a straight line. In Chapter 7 we also considered three more cases: A=C!=0 and B=0, in which case the graph of (1) is a circle; A=B=0 and C!=0, in which case the graph of (1) is a parabola with horizontal axis; and B=C=0 and A!=0, in which case the graph of (1) is a parabola with vertical axis. All cases of equations of type (1) are studied in analytic geometry. In this section we will consider the algebraic solution of certain systems of equations of type (1).
Real solutions of a system of quadratic equations in two variables sometimes can be found by graphing both equations and then estimating the coordinates where their graphs intersect.
Example 1. Solve the system
y=x^2-2x+2
y+x=3
In order to graph
y=x^2-2x+2
we complete the square and write it as
y-1=(x-1)^2
whose graph is a parabola with vertex (1, 1) opening upward. Graphing we obtain
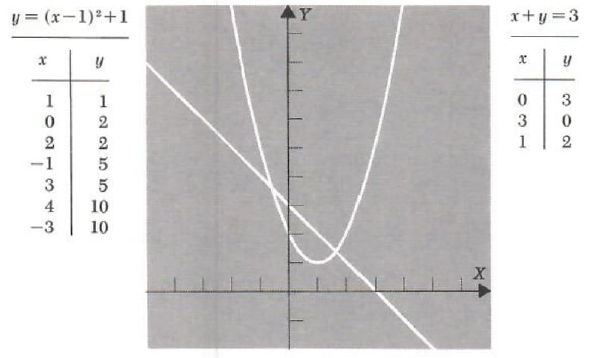
Thus to one decimal place, the two solutions are approximately (-0.6, 3.6) and (1.6, 1.4).
Another technique for solving such a system is the method of substitution. We apply this method to the system in Example 1.
Example 2. Solve the system
y=x^2-2x+2
y+x=3
Solving the second equation for y and substituting, we obtain the system
y = 3 - x
3 - x = x^2 - 2x + 2
Solving the second equation for x: we have
x^2-x-1=0
x=(1+-sqrt(5))/2
We now use the equationy = 3 - x to obtain the corresponding values of y. For x = (1 +sqrt(5))/2,
y = 3 - x
=3-(1+sqrt(5))/2
=(5-sqrt(5))/2
For x = (1 -sqrt(5))/2,
y=3-((1-sqrt(5))/2
= (5+sqrt(5))/2
Thus the solution set of the system is
S={(1/2+sqrt(5)/2,5/2-sqrt(5)/2),(1/2-sqrt(5)/2,5/2+sqrt(5)/2)
Since root(5)≈2.2 to one decimal place, we have the approximation
{(1.6,1.4),(-0.6,3.6)}
which is what we obtained in Example 1.
Example 3. Solve the system
x^2+y^2=13
x+y=5
We solve the second equation for y and substitute in the first equation, which gives us the system
x^2+(5-x)^2=13
y=5-x
Solving the first equation we have
x^2+(5-x)^2=13
x^2+25-10x+x^2=13
2x^2-10x+12=0
x^2-5x+6=0
x^2+(5-x)^2=13
x = 3 or x = 2
For x = 3 we find from the second equation that y= 2 , while for x = 2,y = 3 . Hence our solution set is
S = {(3,2), (2,3)}
The graph of the first equation is a circle with center (0, 0) and radius‘sqrt(13)=3.6, while that of the second equation is a line. Graphing we
have
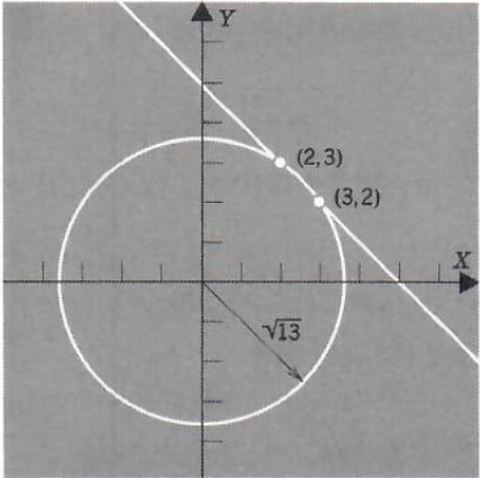
Example 4. Solve the system
2x^2+3y^2=21
3x^2-4y^2=23
We multiply the first equation by 4/3 and add to obtain the system
2x^2+3y^2=21
17/3x^2=51
Solving the second equation for x we have
17/3x^2=51
x^2=9
x=+-3
We substitute each value of x into the first equation. For x=3,
y^2=1
y=+-1
and for x=-3
y^2=1
y=+-1
Thus our solution set is
S={(3,1),(3,-1),(-3,1),(-3,-1)}
Example 5. Solve the system of equations
x-y=4
x^2+y^2-2x-2=0
Solving for y in the first equation and substituting in the second we have
y=x-4
x^2+(x-4)^2-2x-2=0
Solving the quadratic we have
2x^2-10x+14=0
or
x^2-5x+7=0
Using the quadratic formula we obtain
x=(5+-root(25-28))/(2)
=5/2+-(root(3)i)/2
Substituting these values for x in the equation y = x-4, we find that the solution set is
S={(5/2+(root(3)i)/(2),-(3/2)+(root(3)i)/2),(5/2-(root(3)i)/(2),-(3/2)-(root(3)i)/2)}
Since the solutions are pairs of complex numbers, the graphs of the original equations do not intersect.
x^2+y^2-2x-2=0
x^2-2x+1+y^2=2+1
(x-1)^2+y^2=(root(3))^2
| x | yy |
| 0 | -4 |
| 4 | 0 |
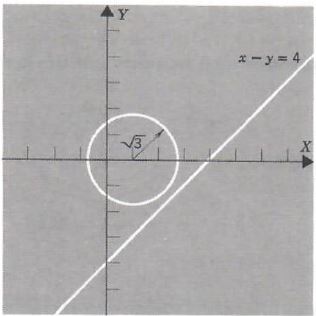
Some other methods for solving systems of quadratic equations in two variables are illustrated in the next few examples.
Example 6. Solve the system
3x^2-4xy+2y^2=3
2x^2-6xy+y^2=-6
Eliminate the constant term in the second equation by multiplying the first equation by 2 and adding. We obtain the system
3x^2-4xy+2y^2=3
8x^2-14xy+5y^2=0
Factor the second equation and solve for y in terms of x.
(4x-5y)(2x-y)=0
Either
4x-5y=0
y=4/5x
or
2x-y=0
y=2x
Substitute these expressions for y into the first equation and solve for x. For y=(4/5)x.
3x^2-4x(4/5x)+2(4/5x)^2=3
x^2=25
x=+-(5/3)
Since y=(4/5)x, we obtain (5/3,4/3) and (-(5/3),-(4/3)). For y=2x.
3x^2-4x(2x)+2(2x)^2=3
3x^2=3
x^2=1
x=+-1
Since y=2x, we obtain (1,2) and (-1,-2). Thus our solution set is
S={(5/3,4/3),(-5/3,-4/3),(1/2),(-1,-2)}
Example 7. Solve the system
x^2+y^2=5
3x^2-2xy+3y^2=11
Multiply the first equation by -3 and add to eliminate both the x^2 and y^2 terms. We obtain the system
x^2+y^2=5
xy=2
Solve the second equation for y in terms of x and substitute back in the
first equation obtaining
x^2+(2/x)^2=5
Solve for x
x^2+4/x^2=5
x^4-5x^2+4=0
(x^2-4)(x^2-1)=0
Either
x^2-4=0
x^2=4
x=+-1
Substituting these values for x in the equation xy=2 we obtain the solution set
S={(2,1),(-2,-1),(1,2),(-1,-2)}
8.10 More Statement Problems
There are statement problems that lead to systems of quadratic equations in two variables. Let us consider some examples.
Example 1. Find all pairs of integers such that the sum of their squares is 170 while their difference is 4.
Step 1. Let x be one integer and y the other.
Step 2. Since the sum of the squares of the two integers is 170,
x^2+y^2=170
Since their difference is 4,
y-x=4
Step 3. Solve the system
x^2+y^2=170
y-x=4
Solve the second equation for y and substitute in the first equation to obtain
y=x+4
x^2+(x+4)^2=170
Solve the second equation for x.
x^2+x^2+8x+16=170
2x^2+8x-154=0
x^2+4x-77=0
(x-7)(x+11)=0
x=7 or x=-11
Using the first equation we obtain as our solution set
S={(7,11),(-11,-7)}
Example 2. Find the dimensions of a rectangle whose area is 120 square feet and whose perimeter is 46 feet.
Step 1. Let x be the length and y be the Width
Step 2. Since the area is 120 square feet
xy=120
Since the perimeter is 46feet.
2x+2y=46
Step 3. Solve the system
xy=120
x+y=23
Solving the second equation for y and substituting in the first equation we obtain the system
y=23-x
x(23-x)=120
Solve the second equation for x
x(23-x)=120
x^2-23x+120=0
(x-8)(x-15)=0
x=8 or x=-15
Using the first equation to solve for y we see that the dimensions are
x=15 feet, y=8 feet
Example 3. A certain group of people rented a bus for $240. If there had been 3 fewer people it would have cost each person $4 more. How many people were there and what was the cost per person?
Step 1. Let x be the number of people in the group and y be the cost per person.
Step 2. Since the cost is $240,
xy=240
If 3 fewer people went, there would have been x-3 people and it would have cost each person 4 dollars more, that is,
y+4 dollars. Therefore,
(x-3)(y+4)=240
Step 3. Solve the system
xy=240
(x-3)(y+4)=240
Simplifying the second equation and using the first equation, we obtain the system
y=240/x
xy-3y+4x-12=240
or
y=240/x
-3(240/x)+4x-12=0
Solving the second equation for x,
-3(240/x)+4x-12=0
-180+x^2-3x=0
x^2-3x-180=0
(x-15)(x+12)=0
x=15 or x=-12
Clearly x=15 people is the only solution since -12 cannot represent a number of people. Since xy=240, we have
x=15 People, y=$16 per person