Rational Forms
CHAPTER 4
Rational Forms
4.1 Introduction
By a rational form we will mean an algebraic expression of the form P/Q, where P and Q are polynomials in one or more variables, and Q is nonzero. The polynomial P will be called the numerator of the rational form and Q will be called the denominator.
In Chapter 1, we pointed out that if a,b, and c are any three real numbers with b!=0, and c!=0, then since c/c = 1 ,
(ac)/(bc)=(a)/(b)(c)/(c)=a/b
This shows us that any nonzero factor may be cancelled from both the numerator and denominator of a fraction. Similarly, to reduce a rational form to lowest terms, we first express the numerator and denominator as products of their prime factors and then cancel the common factors.
Example 1. Simplify (28x^3y^3z^2)/(12xy^2z^3).
(28x^2y^3z^2)/(12xy^2z^3)
=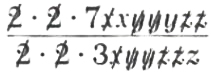
=(7xy)/(3z)
Example 2. Simplify (12a^2x+18a^2y)/(16ax+24ay).
(12a^2x+18a^2y)/(16ax+24ay)
=(6a^2(2x+3y))/(8a(2x+3y))
=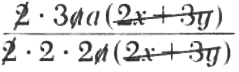
=(3a)/4
Example 3. Simplify (x^2-4a^2)/(2a^2+ax-x^2)
(x^2-4a^2)/(2a^2+ax-x^2)
=((x-2a)(a+2a))/((2a-x)(a+x))
Since (x-2a) and (2a-x) differ only by the factor of (-1), we have
(x^2-4a^2)/(2a^2+ax-x^2)
=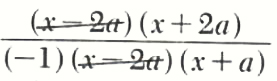
=((x+2a))/((-1)(x+a))
=(x+2a)/(a+a)
In the final step, note that we are using the rule
-(a/b)=-a/b=a/-b
which we recall from Chapter 1.
Since it is so important that we learn how to handle the case when factors differ by the factor of (-1), we will consider two more examples.
Example 4. Simplify (x^2-4x+4)/((2-x)(6-x-x^2)).
(x^2-4x+4)/((2-x)(6-x-x^2))
=((x-2)(x-2))/((2-x)(3+x)(2-x))
=![]()
=1/(x+3)
Let’s see how our math solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.
Example 5. Simplify (x^2-2xy+y^2)/(y^2-xy+x-y).
(x^2-2xy+y^2)/(y^2-xy+x-y)
=((x-y)(x-y))/(y(y-x)-(y-x))
=((x-y)(x-y))/((y-x)(y-1))
=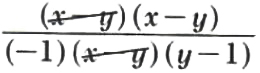
=(x-y)/((-1)(y-1))
=(x-y)/(1-y)
4.2 Multiplication of Rational Forms
If a,b,c, and d are real numbers with b!=0, and d!=0, then,
a/b*c/d=(ac)/(bd)
We apply this rule to rational forms. The product of two rational forms is the rational form whose numerator is the product of the numerators and whose denominator is the product of the denominators. We then simplify the resulting rational form by reducing it to the lowest terms as in the previous section.
Example 1. Multiply (75x)/(64y^2) by (48y^3)/(45x^3) and simplify.
(75x)/(64y^2)*(48y^3)/(45x^3)
=((75x)(48y^3))/((64y^3)(45x^3))
=![]()
=(5y)/(4x^2)
Example 2. Find the product of (a^2+ab-2b^2)/(10a^2b),(5a)/(10a+20b), and (20a^3b^2)/(a-b).
(a^2+ab-2b^2)/(10a^2b)*(5a)/(10a+20b)*(20a^3b^2)/(a-b)
=((a+2b)(a-b))/(2*5aab)*(5a)/(2*5(a+2b))*(2*2*5aaabb)/((a-b))
=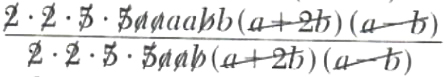
=a^2b
Example 3. Simplify (f^2+2f-8)/(f^2+7f+12)*(f^2+2f-3)/(f^2+f-2)
(f^2+2f-8)/(f^2+7f+12)*(f^2+2f-3)/(f^2+f-2)
=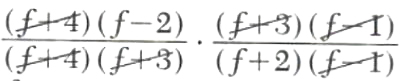
=(f-2)/(f+2)
Example 4. Multiply (s^2-4s+4)/(s^2-9) by (s^2+4s+3)/(s^2-3s+2).
(s^2-4s+4)/(s^2-9)*(s^2+4s+3)/(s^2-3s+2)
=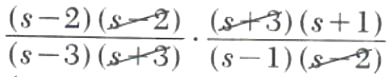
=((s-2)(s+1))/((s-3)(s-1))
Let’s see how our math solver multiplies this and similar problems. Click on "Solve Similar" button to see more examples.
4.3 Division of Rational Forms
If a,b,cand d are real numbers with b!=0,c!=0, and d!=0, then
(a)/(b)÷c/d=a/b*d/c
We apply this rule to rational forms and proceed as in 4.2.
Example 1. Divide (3d)/(4c^2) by (9d^3)/(8c^4).
(3d)/(4c^2)÷(9d^3)/(8c^4)
=(3d)/(4c^2)*(8c^4)/(9d^3)
=(2c^2)/(3d^2)
Note that division in this example is performed by inverting the divisor and multiplying.
Example 2. Simplify (x^2+9x+20)/(x^2+2x-8)÷(x^2-25)/(x^2+x-6)
(x^2+9x+20)/(x^2+2x-8)÷(x^2-25)/(x^2+x-6)
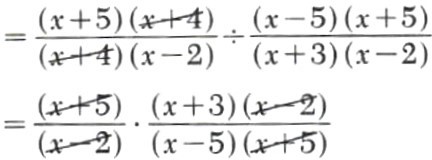
=(x+3)/(x-5)
Let’s see how our math solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.
Example 3. Simplify [(x^2+7xy+10y^2)/(x^2-5xy+6y^2)*(x^2+xy-6y^2)/(x^2-25y^2)÷(x^2+5xy+6y^2)/(x^2-3xy-10y^2)
[(x^2+7xy+10y^2)/(x^2-5xy+6y^2)*(x^2+xy-6y^2)/(x^2-25y^2)÷(x^2+5xy+6y^2)/(x^2-3xy-10y^2)
=[((x+5y)(x+2y))/((x-3y)(x-2y))*((x+3y)(x-2y))/((x-5y)(x+5y))((x-5y)(x+2y))/((x+3y)(x+2y))
=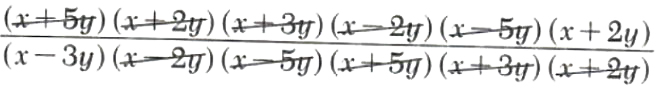
=(x+2y)/(x-3y)
4.4 Addition and Subtraction of Rational Forms
Let us recall from Chapter 1 that to add fractions the first step is to find their L.C.D., that is, the L.C.M., of their denominators. We will review the method of finding the L.C.M. of a set of integers.
Example 1. Find the L.C.M. of 6, 18, and 27.
Since
6=2*3
18=2*3*3
27=3*3*3
we have
L.C.M. (6,18,27)=2*3*3*3=54
Similarly to add rational forms the first step is to find their L.C.D., that is, the L.C.M., of their denominators. To find the L.C.M. of a set of polynomials we proceed just as we did for integers.
Example 2. Find the L.C.M. of 2y+8,3y-6, and y^2+2y-8.
Factor each of the given polynomials
2y+8=2(y+4)
3y-6=3(y-2)
y^2+2y-8=(y+4)(y-2)
Thus, the L.C.M. is
2*3(y+4)(y-2)
Example 3. Find the L.C.M. of 2s+4,3-3s, and s^2+s-2.
2s+4=2(s+2)
3-3s=3(1-s)
s^2+s-2=(s+2)(s-1)
Since s-1=(-1)(1-s), we only use one of these factors in the L.C.M. Therefore, one L.C.M. is
2*3(1-s)(s+2)
while the other L.C.M. is
2*3(s-1)(s+2)
There are always two L.C.M.’s, one being (-1) times the other.
When adding rational forms we first find a common denominator and then express each rational form as an equivalent rational form with this common denominator. The sum is the rational form whose denominator is the common denominator and whose numerator is the sum of the numerators. With this definition, addition of rational forms is performed in the same way as addition of fractions. Therefore, as noted above, the work is simplified if we use the L.C.D., that is, the L.C.M., of the denominators. Subtraction of rational forms is performed in the same way as subtraction of fractions.
Example 4. Compute 1/(5xy^2)+3/(10xy)+1/(15x^2y^3).
We first find the L.C.M. of the denominators.
5xy^2=5xyy
10xy=2*5xy
15x^2y^3=3*5xxyyy
The L.C.M. is
2*3*5xxyyy=2*3*5x^2y^3
Now express each rational form as an equivalent rational form with denominator 2*3*5x^2y^3.
1/(5xy^2)=1/(5xy^2)(2*3xy)/(2*3xy)=(6xy)/(30x^2y^3)
3/(10xy)=3/(10xy)*(3xy^2)/(3xy^2)=(9xy^2)/(30x^2y^3)
1/(15x^2y^3)=1/(15x^2y^3)*2/2=2/(30x^2y^3)
Hence,
1/(5xy^2)+3/(10xy)+1/(15x^2y^3)
=(6xy)/(30x^2y^3)+(9xy^2)/(30x^2y^3)+2/(30x^2y^3)
=(6xy+9xy^2+2)/(30x^2y^3)
Let’s see how our math solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.
Example 4. Simplify 1/(2s+4)+s/(3-3s)+1/(s^2+s-2)
2s+4=2(s+2)
3-3s=3(1-s)
s^2+s-2=(s+2)(s-1)
An L.C.D. is
2*3(s-1)(s+2)
Thus,
1/(2s+4)+s/(3-3s)+1/(s^2+s-2)
=1/(2(s+2))-s/(3(1-s))+1/((s+2)(s-1)
=1/(2(s+2))*(3(s-1))/(3(s-1))-s/(3(1-s))*(2(-1)(s+2))/(2(-1)(s+2))+1/((s+2)(s-1))*(2*3)/(2*3)
=(3(s-1)+2s(s+2)+2*3))/(2*3(s+2)(s-1))
=(3s-3+2s^2+4s+6)/(2*3(s+2)(s-1)
=(2s^2+7s+3)/(2*3(s+2)(s-1))
=((2s+1)(s+3))/(6(s+2)(s-1))
4.5 Complex Fractions
By a complex fraction we mean any fraction whose numerator or denominator (or both) is made up of one or more rational forms. We simplify by first simplifying the numerator, then the denominator, and finally dividing the resulting rational forms. This is illustrated in the following examples.
Example 1. Simplify (1/3-3/2)/(1/4-1/6).
Simplifying the numerator, we have
1/3-3/2=2/6-9/6=-(7/6)
Simplifying the denominator, we have
1/4-1/6=3/12-2/12=1/12
Dividing, we have
(1/3-3/2)/(1/4-1/6)
=(-(7/6))/(1/12)
=-(7/6*12/1)
=-14
Example 2. Simplify (1/y^4-4/y^2+4)/(1/y^2-2)
Simplifying the numerator, we have
1/y^4-4/y^2+4
=1/y^4-(4y^2)/(y^4)+(4y^4)/(y^4)
=(1-4y^2+4y^4)/(y^4)
=((1-2y^2)^2)/y^4
Simplifying the denominator, we have
1/y^2-2
=1/y^2-(2y^2)/(y^2)
=(1-2y^2)/y^2
Dividing, we have
(1/y^4-4/y^2+4)/(1/y^2-2)
=(((1-2y^2)^2)/(y^4))/((1-2y^2)/(y^2))
=((1-2y^2)^2)/(y^4)*(y^2)/((1-2y^2))
=(1-2y^2)/y^2
Example 3. Simplify 1/(1-1/(1+1/x))
The numerator is already simplified. To simplify the denominator, we must first simplify 1/(1+1/x)
1/(1+1/x)
=1/(x/x+1/x)
=1/((x+1)/x)
=1*x/(x+1)
=x/(x+1)
Thus, the denominator is
1-1/(1+1/x)
=1-x/(x+1)
=(x+1)/(x+1)-x/(x+1)
=(x+1-x)/(x+1)
=1/(x+1)
Dividing, we have
1/(1-1/(1+1/x))
=1/(1/(x+1))
=(x+1)/1
=x+1
Example 4. Simplify (x/(x+y)-(y-x)/x)/(x/(x+y)+(y-x)/x)
Simplify the numerator.
x/(x+y)-(y-x)/x
=(x^2)/((x+y)x)-((y-x)(x+y))/(x(x+y))
=(x^2-(y^2-x^2))/(x(x+y))
=(2x^2-y^2)/(x(x+y))
Simplify the denominator.
x/(x+y)+(y-x)/x
=x^2/(x(x+y))+((y-x)(x+y))/(x(x+y))
=(x^2+y^2-x^2)/(x(x+y))
=y^2/((x(x+y))
Divide.
(x/(x+y)-(y-x)/x)/(x/(x+y)+(y-x)/x)
=((2x^2-y^2)/(x(x+y)))/((y^2)/(x(x+y)))
=(2x^2-y^2)/(x(x+y))*(x(x+y))/(y^2)
=(2x^2-y^2)/(y^2)
Another method for simplifying complex fractions is to find the L..C.M. of all the denominators and multiply both numerator and denominator of the complex fraction by this L.C.M. We will rework Examples 2 and 4 above to illustrate this method.
Example 5. Simplify (1/y^4-4/y^2+4)/(1/y^2-2)
The rational expressions are 1/y^4, 4/y^2, 4, 1/y^2, and 2, and the L.C.M. of the denominators of these expressions is y^4. Thus,
(1/y^4-4/y^2+4)/(1/y^2-2)
=(1/y^4-4/y^2+4)/(1/y^2-2)*(y^4/y^4)
=(1-4y^2+4y^4)/(y^2-2y^4)
=(1-2y^2)/(y^2)
Example 6. Simplify (x/(x+y)-(y-x)/x)/(x/(x+y)+(y-x)/x).
The denominators are x+ y, x, x+ y, and x, and the L.C.M. is x(x + y).
Thus,
(x/(x+y)-(y-x)/x)/(x/(x+y)+(y-x)/x)
=(x/(x+y)-(y-x)/x)/(x/(x+y)+(y-x)/x)*(x(x+y))/(x(x+y))
=(x/(x+y)*(x(x+y))/(1)-(y-x)/x*(x(x+y))/1)/(x/(x+y)*(x(x+y))/1+(y-x)/x*(x(x+y))/1)
=(x^2-(y-x)(x+y))/(x^2+(y-x)(x+y))
=(x^2-y^2+x^2)/(x^2+y^2-x^2)
=(2x^2-y^2)/y^2