The circle and symmetry

The circle and symmetry

  In Section 3.3 we studied the graphs of quadratic relations in which one of the variables was first-degree and the other was second-degree. Three important kinds of relations involve equations in which both variables are second-degree: circles, ellipses. and hyperbolas. In this section we look at circles, and in the next we study the other two.

  We will start with the geometric definition of a circle and use the distance formula to derive the equation of the corresponding relation. This is similar to the way we derived the equation of a quadratic relation from the geometric definition of a parabola in Section 3.3. From now on we will refer to both the relation and its graph as the circle.

CIRCLES By definition. a circle is the set of all points in a plane that lie a given distance from a given point. The given distance is the radius of the circle and the given point is the center. Since a circle is a set of points. it corresponds to a relation. The equation of a circle can be found from its definition by using the distance formula.
  Figure 3.28 shows n circle of radius 3 with center at the origin. To find the equation of this circle, let (x, y) be any point on the circle. The distance between (x, y) and the center of the circle, (0, 0). is given by

  root((x-0)^2+(y-0)^2

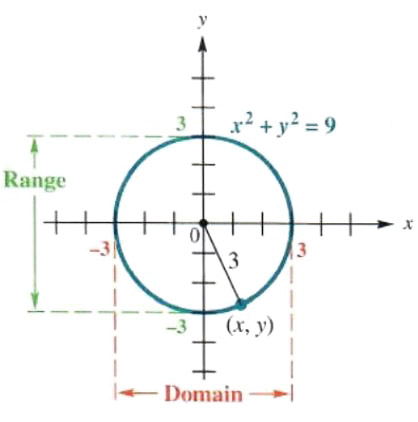
  Figure 3.28

  Since this distance equals the radius, 3.

  As suggested by Figure 3.28, the domain of the relation is -3,3. and the range of the relation is -3,3.

Example 1

FINDING THE EQUATION OF A CIRCLE

  Find an equation for the circle having radius 6 and center at (-3, 4). Graph the circle.

  This circle is shown in Figure 3.29. Its equation can be found by using the distance formula. Let (x, y) be any point on the circle. The distance from (x, y) to (-3, 4) is given by

  root([x-(-3)]^2+(y-4)^2)=root((x+3)^2+(y-4)^2)

  This same distance is given by the radius, 6. Therefore,

  root((x+3)^2+(y-4)^2)=6

  or  (x+3)^2+(y-4)^2=36

  The domain is -9,3, and the range is -2,10, as seen in Figure 3.29. 

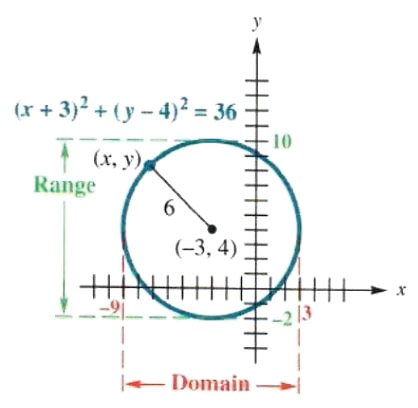
  Figure 3.29

  Generalizing from the work in Example 1 gives the following result.

CENTER-RADIUS FORM OF THE EQUATION OF A CIRCLE

  

Example 2

FINDING THE CENTER AND THE RADIUS BY COMPLETING THE SQUARE 

  Find the center and radius for x^2 - 6x + y^2 + 10y + 25 = 0.
Since this equation has the form of equation (*) above, it represents either a circle, a single point, or no points at all. To decide which, complete the square on x and y separately. Start with 

  (x^2-6x)+(y^2+10y)=-25

  Half of -6 is -3, and (-3)^2= 9. Also, half of 10 is 5 , and 5^2=25. Add 9 and 25 on the left, and to compensate, add 9 and 25 on the right:

  (x^2-6x+9)(y^2+10y+25)=-25+9+25

  (x-3)^2+(y+5)^2=9

  Since 9 > 0, the equation represents a circle with center at (3, -5) and radius root(9)=3.

  In Section 3.3 we saw how the graph of y = x^2 can be translated up, down, right, or left by adding or subtracting constants on the right side. This procedure of translation can be extended to other types of graphs. The next example shows how this is done with a circle.

Example 3

EXAMINING A TRANSLATION OF A CIRCLE

  (a) Graph x^2+y^2=16.

  This is the equation of a circle with center at (0, 0) and radius root(16)=4. See Figure 3.31(a).

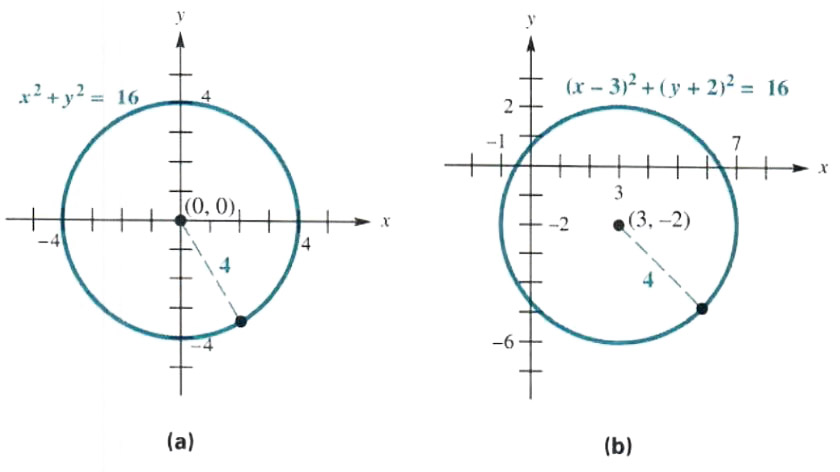
  FIGURE 3.31

  (b) Graph (x - 3)^2 + (y + 2)^2 = 16.

  By the center-radius form of the equation of a circle, this relation is a circle with center at (3, -2) and radius 4. The graph is shown in Figure 3.31(b).

  (c) Compare the graphs in Figures 3.31 (a) and (b).

  The graph of (x-3)^2+(y+2)^2=16 is the same as that of x^2 + y^2 = 16, except that it has been translated 3 units to the right (due to (x - 3)) and 2 units down (due to (y+2)=y-(-2)).

  Generalizing from Example 3, we can make the following observations concerning the graph of (x - h)^2 + (y - k)^2 = r^2(r > 0).

Let’s see how our math solver generates graph for this and similar problems. Click on "Solve Similar" button to see more examples. 

TRANSLATIONS OF A CIRCLE

  The graph of the circle (x - h)^2 + (y - k)^2 = r^2(r > 0) is the same as the graph of x^2 + y^2 = r^2, with the following translations:

  1. h units to the right if h > 0;|h| units to the left if h < 0

  2. k units up if k > 0; |k| units down if k < 0

IN SIMPLEST TERMS

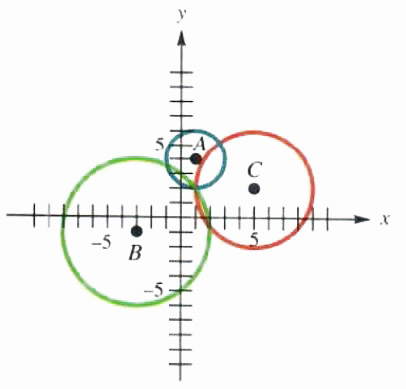
  Seismologists can locate the epicenter of an earthquake by determining the intersection of three circles. The radii of these circles represent the distances from the epicenter to each of three receiving stations. The centers of the circles represent the receiving stations.

  Suppose receiving stations A, B, and C are located on a coordinate plane at the points (1, 4), (-3, -1), and (5, 2). Let the distance from the earthquake epicenter to each station be 2 units, 5 units, and 4 units, respectively. Where on the coordinate plane is the epicenter located?

  Graphically, it appears that the epicenter is located at (1, 2). To check this algebraically, determine the equation for each circle and substitute x = 1 and y = 2.

  Station 1:

  (x-1)^2+(y-4)^2=4

  (1-1)^2+(2-4)^2=4

  0+4=4

  4=4

  Station 2:

  (x+3)^2+(y+1)^2=25

  (1+3)^2+(2+1)^2=25

  16+9=25

  25=25

  Station 3:

  (x-5)^2+(y-2)^2=16

  (1-5)^2+(2-2)^2=16

  16+0=16

  16=16

  Thus, we can be sure that the epicenter lies at (1, 2).

SYMMETRY In Section 3.3 we discussed the axis of symmetry of a parabola. For example, the axis of symmetry of the graph of y = -(x + 3)^2 + 1 is the
vertical line x = -3 (see Figure 3.21 in Section 3.3), because if the graph were folded along this line, the two halves would coincide. The idea of symmetry is helpful in drawing graphs, and can be extended to other graphs as well.

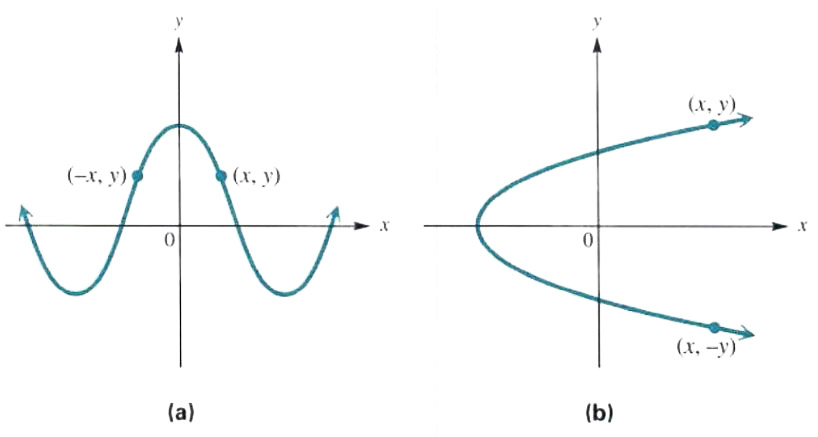
  Figure 3.32

  Figure 3.32(a) shows a graph that is symmetric with respect to the y-axis. As suggested by Figure 3.32(a), for a graph lo be symmetric with respect to the y-axis, the point (-x, y) must be on the graph whenever (x, y) is on the graph.

Similarly, if the graph in Figure 3.32(b) were folded in half along the x-axis, the portion from the top would exactly match the portion from the bottom. Such a graph is symmetric with respect to the x-axis. As the graph suggests, symmetry with respect

  to the x-axis means that the point (x, - y) must be graph whenever the point (x, y) is on the graph.

  The following tests tell when a graph is symmetric with respect to the x-axis or y-axis.

SYMMETRY WITH RESPECT TO AN AXIS

  The graph of an equation is symmetric with respect to the y-axis if the replacement of x with -x results in an equivalent equation.

  The graph of an equation is symmetric with respect to the x-axis if the replacement of y with -y results in an equivalent equation.

Example 4

TESTING FOR SYMMETRY WITH RESPECT TO AN AXIS

  Test for symmetry with respect to the x-axis or y-axis.

  (a) y=x^2+4

  Replace x with -x:

  y=x^2+4

  becomes

  y=(-x)^2+4=x^2+4.

  The result is the same as the original equation, so the graph (shown in Figure 3.33) is symmetric with respect to the y-axis. The graph is not symmetric with respect to the x-axis, since replacing y with -ygives

  -y=x^2+4,

  which is not equivalent to the original equation.

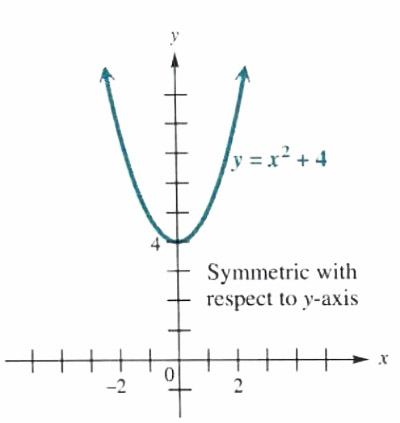
  Figure 3.33

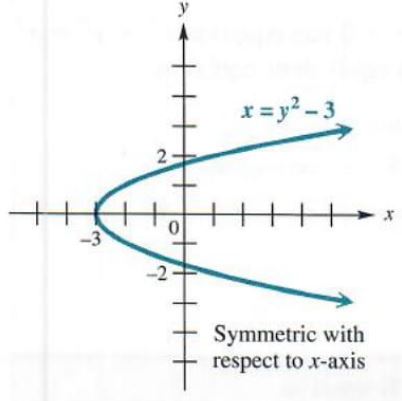
  Figure 3.34

  (b) x = y^2 - 3

  Replace y with -y to get x=(-y)^2-3=y^2-3. the same as the original equation. The graph is symmetric with respect to the x-axis. as shown in Figure 3.34. The graph is not symmetric with respect to the y-axis because -x=y^2-3 is not equivalent to x = y^2 - 3.

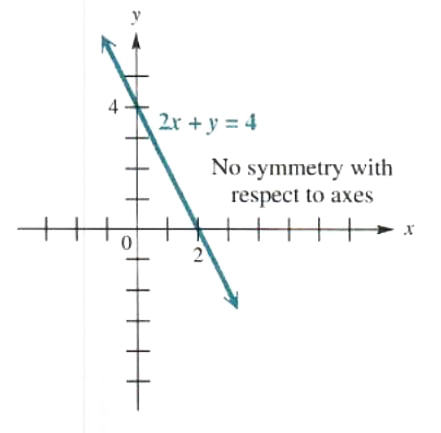
  Figure 3.5

  c) 2x+y=4

  Replace x with -x and then replace y with -y; in neither ease does an equivalent equation result. This graph is symmetric neither with respect to the x-axis nor the y-axis. See Figure 3.35. 

  Another kind of symmetry is found when it is possible to rotate a graph 180^0 about the origin and have the result coincide exactly with the original graph. Symmetry of this type is called symmetry with respect to the origin. It can be shown that rotating a graph 180^0 is equivalent to saying that the point (-x,-x) is on the graph whenever (x, y) is on the graph. Figure 3.36 shows two graphs that are symmetric with respect to the origin. A test for this type of symmetry is given below.

SYMMETRY WITH RESPECT TO THE ORIGIN

  The graph of an equation is symmetric with respect to the origin if the replacement of both x with -x and y with -y results in an equivalent equation.

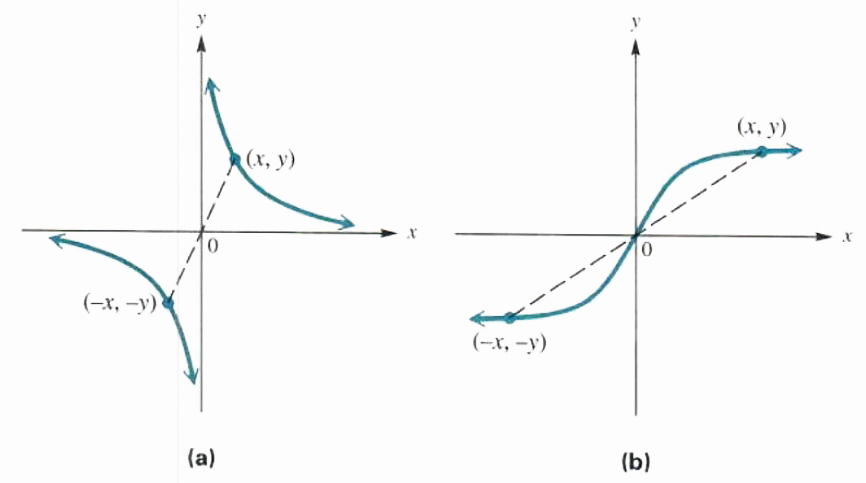
  Figure 3.36

Example 5

TESTING FOR SYMMETRY WITH RESPECT TO THE ORIGIN 

  Show algebraically that a circle with center at the origin is symmetric with respect to the origin. (See Figure 3.30.)

  A circle with center at the origin and radius r>0 has equation x^2+y^2=r^2.

  By substituting -x for x and -y for y. we get an equivalent equation.

  x^2+y^2=r^2  Original equation

  (-x)^2+(-y)^2=r^2  Replace x with -x, y with -y.  Equivalent to original equation