Command Join fractions Expression
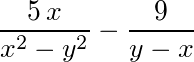 
- A sum that comprises 2 terms. The 1st term of the sum is equal to a fraction: the numerator of the fraction is a product that consists of 2 factors. The 1st factor of the product is five. The 2nd factor of the product is equal to x. The denominator of the fraction is a sum consisting of 2 terms. The 1st term of the sum is equal to a power. The base is x. The exponent is two. The 2nd term of the sum is a negative power. The base is y. The exponent is two. The 2nd term of the sum is equal to a negative fraction: the numerator of the fraction is nine. The denominator of the fraction is a sum that contains 2 terms. The 1st term of the sum is equal to y. The 2nd term of the sum is equal to negative x.
- five times x fraction line x to the power two plus negative y to the power two plus negative nine divided by y plus negative x;
Result
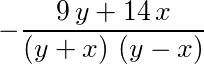 
- A rational expression: the numerator of the rational expression is a negative sum comprising 2 terms; the 1st term of the sum is equal to a product that comprises 2 factors; the 1st factor of the product is equal to nine; the 2nd factor of the product is equal to y; the 2nd term of the sum is a product that comprises 2 factors; the 1st factor of the product is fourteen; the 2nd factor of the product is x; the denominator of the rational expression is a product that comprises 2 factors; the 1st factor of the product is a sum that comprises 2 terms; the 1st term of the sum is equal to y; the 2nd term of the sum is x; the 2nd factor of the product is equal to a sum that contains 2 terms; the 1st term of the sum is y; the 2nd term of the sum is equal to negative x;
- negative open parenthesis nine times y plus fourteen times x close parenthesis fraction line left bracket y plus x right bracket times opening brace y plus negative x closing brace.
|