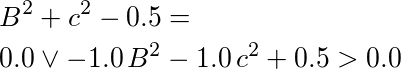QuickMath Download on App Store Download on Google Play
Welcome to Quickmath Solvers! Download on App Store Download on Google Play
Created on: 2012-02-09

A sample problem solved by Quickmath online math calculator

5/(7*a^4)-1/(14*a)/2/(3*a^2) simplified | (5*p-4)/6-(2*p+3)/2 = 7 equation solved

Command

Solve

Inequality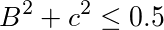
B^2+c^2 <= 0.5

  1. an inequality in which left side of inequality smaller than or equal to right side of inequality; the left side of the inequality is a sum comprising 2 terms; the 1st term of the sum is a power; the base is B; the exponent is two; the 2nd term of the sum is a power; the base is c; the exponent is two; the right side of the inequality is equal to zero point and five tenth;
  2. B raised to the power of two plus c exponentiated by two smaller or equal than zero point five.
Variable
Result
A nonpolynomial inequality has been used, so the solution set may be incorrect.

Exact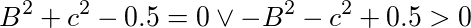

<<B^2+c^2-0.5 = 0>> or <<-B^2-c^2+0.5 > 0>>

  1. an inequality in which left side of inequality larger than right side of inequality. The left side of the inequality is a sum of 3 terms. The 1st term of the sum is equal to a negative power. The base is B. The exponent is two. The 2nd term of the sum is equal to a negative power. The base is c. The exponent is two. The 3rd term of the sum is zero point and five tenth. The right side of the inequality is zero.
  2. opening parenthesis negative B to the power of two plus negative c raised to the power of two plus zero point five greater than zero closing parenthesis.


Approximate

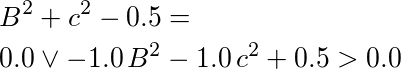
<<B^2+c^2-0.5 = 0.0>> or <<-1.0*B^2-1.0*c^2+0.5 > 0.0>>

  1. an inequality in which left side of inequality larger than right side of inequality; the left side of the inequality is equal to a sum comprising 3 terms; the 1st term of the sum is a product consisting of 2 factors; the 1st factor of the product is equal to negative one; the 2nd factor of the product is equal to a power; the base is B; the exponent is two; the 2nd term of the sum is equal to a negative product consisting of 2 factors; the 1st factor of the product is equal to one; the 2nd factor of the product is equal to a power; the base is c; the exponent is two; the 3rd term of the sum is equal to zero point five; the right side of the inequality is equal to zero;
  2. opening parenthesis negative one times B exponentiated by two plus negative one times c raised to the power of two plus zero point and five tenth larger than zero closing parenthesis.