Concepts of Sets
Introduction
Knowledge of mathematics has become essential in so many fields of endeavor and in so many walks of life that existence without some acquaintance with at least elementary mathematics is exceptionally difficult.
The principles of mathematics have been utilized since the dawn of civilization. The building of the Pyramids at Giza in Egypt over 5000 years ago is a monument to the mathematical skill of Egyptian engineers. Although they had only the simplest tools, they measured and built brilliantly. They constructed geometric figures from lines, laid out right angles. and established a measuring unit called a cubit (about 202/3 inches).
Arithmetic begins with the need for the concept of counting. Although it is virtually impossible to establish exactly when counting came into use, we know the Egyptian hieroglyphic system of numbers dates back as early as 3000 B.C.
Some tribes today have no words at all for numbers, while others lump together all quantities above 1 or 2 as “many.” We assume that this is how numbers started. Once quantities were recognized and named, the next step was learning that the same numbers can be used to count any collection of objects. Even today, in some countries, different sets of numbers are used to count different kinds of things, such as people, animals, days, or trees. Equally important was learning to tally, to keep track, by turning down fingers on the hands or by putting pebbles in a bag. Tallying on fingers led to our base-10 number system. Probably one of the earliest and most important tallies was counting of flocks so that a shepherd might know when a lamb was lost or a camel was born. It was through the necessity and desire to know exactly “how many” in words, and then in symbols, that systems of numeration were developed.
The Egyptian hieroglyphic system of numeration had symbols for the numbers 1, 10, 100, 1000, etc. The Egyptians used the repetitive principle in expressing numbers between 1 and the base, which is 10, and between powers of the base. They wrote the symbols without any definite order.
The Romans, like the Egyptians, used the repetitive principle in their base-10 system of numeration. Unlike the Egyptians, the Romans used the concept of order in their scheme. They modified their system by introducing symbols for the numbers 5, 50, etc., the intermediate steps of the base.
The Hindu-Arabic system of numeration started with nine symbols to represent the numbers 1 through 9 inclusive. The concept of zero came much later and was invented to express the count number of a depleted collection of objects. For thousands of years mathematicians left a space in the middle of a number to show a zero. Around 300 B.C. a dot was used to mark the empty place. The dot is the symbol used for the number zero in Arabic even to the present day. The Hindu Arabic system of numeration is a base-10 system. Unlike the Egyptian hieroglyphic system and the Roman system, the Hindu-Arabic system is a place value system.
Today we use an extension and modernization of the Hindu-Arabic system. We use ten digit symbols to represent numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. These are combined in a place value system to represent any number we may care to express.
When we write a number such as 273, the 3 is in the units place, the 7 is in the tens place, and the 2 is in the hundreds place. That is, there are 3 units, 7 tens, and 2 hundreds.
The numbers 1, 2, 3, etc. are called counting numbers or natural numbers. The number 0, 1, 2, etc. are called whole numbers.
The Number Line
Sometimes it is convenient to use geometry to illustrate some important results in algebra. We would like to have a geometrical representation of the whole numbers. To accomplish this, we draw a straight line and choose a point on the line to represent the number zero. We call this point the origin. Take another point on the line at some distance from the origin to the right of it. Associate that point with the number 1. The segment of the line from the origin to the point representing the number 1 is our unit measurement, and is the scale we use on the line. Now, at a distance of one unit to the right of the point representing the number 1, put another point and let it represent the number 2. We continue this procedure as far as we like, thus establishing an association between the whole numbers and points on the line.

Figure 1.1 shows the number line. The arrow at the end of the line indicates that we continue in this manner and also in the direction of increasing numbers. The segment of the line representing a unit distance, that is, the scale on the line, is taken to suit our purpose (see Figure 1.2).
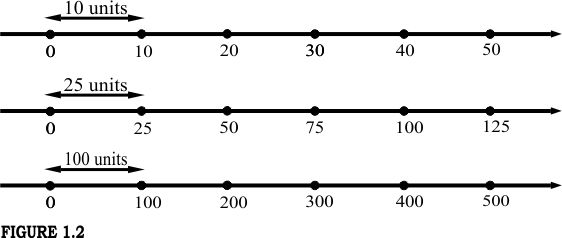
By taking a convenient scale and extending the line far enough, any whole number can be associated with a unique point on the line. The points on the line are called the graph of the numbers. The numbers are called the coordinates of the points.
Note If a and b are the coordinates of any two points on the line, and if the graph of b lies to the right of the graph of a, then b is greater than a, denoted by b > a, or a is less than b, denoted by a < b.
To graph some numbers, draw a line and select an origin. Take a convenient unit distance and show the numbers associated with a few consecutive segments of the number line just to establish the scale. Remember that the same scale must be used over the entire number line.
Example
Plot the graph of the numbers 4, 8, 10, 12, 16.
Solution
Take every unit segment of the line to represent 2 (see Figure 1.3).

To read the coordinates of points on a number line, first determine the scale being used, that is, how much each unit segment of the line represents.
Example
From the number line shown in Figure 1.4 find the coordinates of the circled points.
Solution
Each division of the given number line represents 25; thus the coordinates of the circled points are 150, 275, 325, 425, 475.

Definitions and Notation
The concept of a set has been utilized so extensively throughout modern mathematics that an understanding of it is necessary for all college students. Sets are a means by which mathematicians talk of collections of things in an abstract way.
According to G. Cantor (1845-1918), the mathematician who developed set theory, “a set is a grouping together of single objects into a whole.”
Note that no uniform property of the objects in the set is implied other than that they are grouped together to form the set.
The totality of students taking elementary algebra forms a set. The collection consisting of a pen, a chair, and a flower constitutes a set.
The numbers 1, 2, 3 etc. constitute a set called the set of natural numbers, which is denoted by N. The numbers 0, 1, 2, 3 etc., constitute the set of whole numbers, denoted by W.
There are two ways to define a set. The first is to list and separate by commas the objects that compose the set. We write the defining list within braces { }.
Thus A = {Mars, Venus, Neptune} and N = {1, 2, 3, . . . }. The three dots indicate that we continue in the same manner.
Note It is usual to let capital letters signify sets and lowercase letters represent objects of sets.
If X={a, b, c, d}, then a, b, c, and d are called members or elements of the set X. The notation a {is-in} X is read “a is an element of the set X.”
To denote that the object e is not an element of the set X, we write e {not-in} X.
Note The order of the elements of the set is immaterial. For example, {1 , 2, 3} and {3, 1, 2} define the same set. It is not necessary, but merely convenient, to list numbers in numerical order.
Note When we list the members of a set, each element should be listed only once, since we would otherwise be referring to the same member of the set more than once. The set of numerals in the number 83,837 is {3, 7, 8}.
The second way to define a set is to give the rule that identifies the elements of the set.
We still write the defining rule within braces.
E = {all natural numbers that are a multiple of 2}
Definition
| A variable is a letter that assumes various values in a problem. |
When the set is defined by a rule, the rule may be written in words or, to make it short, in symbols.
To designate a generic member of a set of numbers, a variable such as x, y, 2, m, n, . . . is used.
The set X whose elements have property P is denoted by X = {x | x has property P} which is read “X is the set of elements x, such that x has the property P.” The vertical bar in the notation is an abbreviation for the words “such that.”
Example
List the elements in the set X = {x | x = 2n, n {is-in} W}.
First find the values that n takes.
n takes the values 0, 1, 2, 3, . . .
Find the values that 2n takes (2n means 2 x n).
2n is obtained by multiplying 0, 1, 2, . . . each by 2.
Thus x = 2n takes the values 0, 2, 4, 6, . . .
Hence X= {0, 2, 4, 6, . . .}
Note {x | x = 2n, n {is-in} W} can be written as {2n | n {is-in} W}.
Example
List the elements in the set X = {x | x = 2n - 1, n {is-in} N}.
Find the values that n takes.
n takes the values 1, 2, 3, 4, . . .
Find the values that 2n takes.
2n takes the values 2, 4, 6, 8, . . .
Find the values that 2n - 1 takes.
x=2n- 1 takes the values 1, 3, 5, 7, . . .
Thus X= {1, 3, 5, 7, ...}
Note By 2 < x < 8, x {is-in} N is meant the natural numbers between 2 and 8. That is, x takes the values 3, 4, 5, 6, 7.
Example
List the elements in the set X = {3x | 0 < x < 10, x {is-in} n}:
x takes the values 1, 2, 3, 4, 5, 6, 7, 8, 9
3x takes the values 3, 6, 9, 12, 15, 18, 21, 24, 27
Thus X= {3, 6, 9, 12, 15, 18, 21, 24, 27}
Definition
| The set that has no elements is called the null set and is denoted by ∅ . |
Example
The set of natural numbers between 1 and 2 is the null set. The set of natural satellites of the planet Venus is the null set.
Subsets
Definition
| A set A is a subset of the set B if every element of A is an element of B. |
If A is a subset of B, we write A {subset} B.
Note Every set is a subset of itself.
Examples
1. If A= {1,2,3} and B= {1, 2, 3, 4}, then A {subset} B.
2. The subsets of the set {1 , 2, 3} are {1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3}, {empty}
Note The null set is a subset of every set.
The notation A ⊄ B is read “A is not a subset of B.” This means there exists at least one element in A that is not in B.
Example
If A = {a, b, c} and B = {1,2, a, b}, then A ⊄ B.
Definition
| Two sets A and B are equal, A = B, if every element of A is an element of B and every element of B is an element of A. |
Note A = B means that the relations A ⊂ B and B ⊂ A hold simultaneously.
Example
If A = {1, 2, 3} and B = {3, 1, 2}, then A = B.
The notation A != B, read “A is not equal to B,” means that either there exists at least one element that is a member of A but not of B, or at least one element that is a member of B but not of A.
Example
When A = {1, 3, 5} and B = {1, 2, 3, 5}, then A != B (but A ⊂ B).
Operations with Sets
Definition
|
The union of two sets A and B, denoted by A {union} B, is the set of all elements that are in the set A or in the set B. It is the set of elements that belong to at least one of the two sets. A ∪ B = {x | x ∈ A or x ∈ B} |
Example
1. Let A = {1, 2, 3} and B = {1, 3, 5};
then A ∪ B = {1,2,3,5}
2. Let A = {2, 4, 6} and B = {a, b, c};
then A ∪ B = {2, 4, 6, a, b, c}
Note For any two sets A and B,
1. A ⊂ A ∪ B 2. B ⊂ A ∪ B
3. A ∪ B = B ∪ A 4. A ∪ {empty} = A
Definition
|
The intersection of two sets A and B, denoted by A ∩ B, is the set of elements that are only in both A and B. A ∩ B = {x | x ∈ A or x ∈ B} |
Example
1. If A = {1, 2, 3} and B = {1, 3, 5},
then A ∩ B={1,3}
2. If A = {a, b, c} and B = {d, e, f},
then A ∩ B = {empty}
Definition
| Two sets A and B are disjoint if A ∩ B = {empty} |
Note For any two sets A and B,
1. A ∩ B ⊂ A 2. A ∩ B ⊂ B
3. A ∩ B = B ∩ A 4. A ∩ {empty} = {empty}
Example
Given A = {x l 0 < x < 0, x ∈ N} and
B = {3x | 0 < x< 6, x ∈ N},
find A ∪ B and A ∩ B
Solution
The set A = {1, 2, 3, 4, 5, 6, 7, 8, 9}. The set B = {3, 6, 9, 12, 15}.
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 15}
A ∩ B = {3, 6, 9}
Definition
| The set that contains all the elements under discussion is called the universal set, and is usually denoted by U. |
Example
If A = {1, 2, 3, 4}, B = {4, 6, 8}, C = {8, 11, 14}, and
A, B, C comprise the set U,
then U = {1, 2, 3, 4, 6, 8, 11, 14}