Division of Polynomials
Division of Polynomials
The following are some of the properties pertaining to fractions. These properties are discussed in Chapter 2.
1. a/b = ac/bc 2. (a+b)/c = a/c + b/c
3. a/b*c/d = ac/bd 4. a/b÷c/d = a/b * d/c
Note Since division by zero is not defined, all denominators are assumed different from zero
First we will discuss division of monomials, then division of a polynomial by a monomial, and finally division of two polynomials.
Division of Monomials
From the properties of fractions and the rules governing exponents we have
a^8/a^5 = (a^5*a^3)/(a^5*1) = (a^3)/1 = a^3
=a^(8-5)
a^4/a^4= 1
a^7/a^10 = (a^7*1)/(a^7*a^3) = 1/a^3
=1/a^(10-7)
THEOREM 4

Proof a^m/a^n = (a^n * a^(m-n))/(a^n*1) = a^(m-n) When m>n
a^m/a^n = a^n/a^n = 1 When m=n
a^m/a^n = (a^m*1)/(a^m* a^(n-m)) = 1/a^(n-m) When m
2. a^7/a^5 = a^(7-5) = a^2
3. (a - 1)^4/(a - 1)^3 = (a - 1)^(4-3) = (a - 1)
4. 5^4/5^4 = 1
5. (x +1)^3/(x + 1)^3 = 1
6. 3^8/3^12 = 1/3^(12-8) = 1/3^4
7. a^3/a^9 = 1/a^(9-3) = 1/a^6
8. (x + 2)^4/(x + 2)^6 = 1/((x + 2)^(6-4) = 1/(x + 2)^2
From the properties of fractions and the definition of exponents we have
(2/3)^4 = 2/3*2/3*2/3*2/3
= (2*2*2*2)/(3*3*3*3)
= 2^4/3^4
Let's see how our Polynomial solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.
THEOREM 5
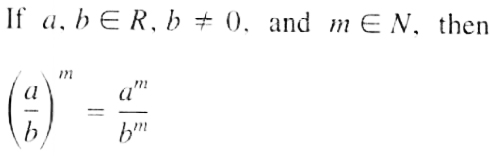
Proof
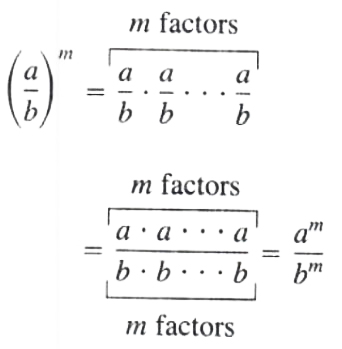
COROLLARY
![]()
then by the use of Theorem 2 and Theorem 3 and theorem 5, we have
((a^(m)b^(n))/(c^(p)d^(q)))^k = ((a^(m)b^(n))^k)/((c^(p)d^(q))^k = (a^(mk)b^(nk))/(c^(pk)d^(qk))
EXAMPLE Simplify (-30a^3b^2)/(12a^2b^4) by applying the laws of exponents.
Solution (-30a^3b^2)/(12a^2b^4) = -((2*3*5a^3b^2)/(2*2*3a^2b^4))
=-((2*3)/(2*2))*(5/2)*(a^3/a^2)*(b^2/b^4)
=-(5/2)*(a/1)*(1/b^2)
=-((5a)/(2b^2))
Let's see how our Polynomial solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.
EXAMPLE By applying the laws of exponents, simplify [(2x^4yz)/(6xy^2)]^3
Solution We can simplify the fraction first before applying the outside exponent.
[(2x^4yz)/(6xy^2)]^3 = [(x^3z)/(3y)]^3 = (x^9z^3)/(3^3y^3) = (x^9z^3)/(27y^3)
EXAMPLE 12^4/18^3 = (2^2*3)^4/(2*3^2)^3 = (2^8*3^4)/(2^3*3^6)
=(2^8/2^3)*(3^4/3^6) = (2^5/1)*(1/(3^2)) = 32/9
EXAMPLE Simplify ((2a^2bc^3)^3)/((3ab^2)^2) by applying the laws of exponents
Solution Here we cannot simplify first. since the numerator and the denominator have different powers. Apply the outside exponents first. then simplify,
((2a^2bc^3)^3)/((3ab^2)^2) = (2^3a^6b^3c^9)/(3^2a^2b^4) = (8a^4c^9)/(9b)
Let's see how our Polynomial solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.
EXAMPLE Perform the indicated operations and simplify:
16a^4b^3÷(-2ab)^3 + 36a^5b^2÷(-3a^2b)^2
Solution 16a^4b^3÷(-2ab)^3 + 36a^5b^2÷(-3a^2b)^2
=(16a^4b^3)/(-2ab)^3 + (36a^5b^2)/(-3a^2b)^2
=(16a^4b^3)/(-2^3a^3b^3) + (36a^5b^2)/(3^2a^4b^2)
=(16a^4b^3)/(-8a^3b^3) + (36a^5b^2)/(9a^4b^2)
=-2a + 4a = 2a
Division of a Polynomial by a Monomial
From the properties of fractions we have
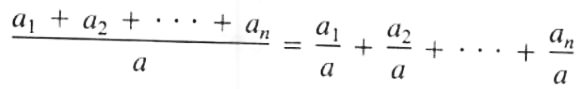
Keep in mind that
(a + b)/c means (a+b)÷c
![]() but
but
(a + b)/a = a/a + b/a = 1 + b/a
To divide a polynomial by a monomial, divide every term of the polynomial by the monomial.
EXAMPLE Divide (12x^3 - 6x^2 + 18x)/6x and simplify.
Solution (12x^3 - 6x^2 + 18x)/(6x) = (12x^3)/(6x) + (-6x^2)/(6x) + (18x)/(6x)
=2x^2 - x + 3
Let's see how our Polynomial solver simplifies this and similar problems. Click on "Solve Similar" button to see more examples.
EXAMPLE Divide (3a^3 - 2a^2b - ab^2)/(-ab) and simplify.
Solution (3a^3 - 2a^2b - ab^2)/(-ab) = (3a^3)/(-ab) + (-2a^2b)/(-ab) + (-ab^2)/(-ab)
=-((3a^2)/b) + 2a + b
EXAMPLE Perform the indicated operations and simplify:
(12a^4 + 4a^3 - 32a^2)/(4a^2) - (3a - 8)(a + 1)
Solution (12a^4 + 4a^3 - 32a^2)/(4a^2) - (3a - 8)(a + 1)
=(3a^2 + a - 8) - (3a^2 - 5a - 8)
=3a^2 + a - 8 -3a^2 + 5a + 8 = 6a
Division of Two Polynomials
Division is defined as the inverse operation of multiplication; thus we start with a multiplication problem and then deduce the division operation.
(x^2 + 3x -5)(2x -7) = x^2(2x - 7) + 3x(2x - 7) + (-5)(2x - 7)
=2x^3 - 7x^2) + (6x^2 -21x) + (-10x + 35)
=2x^3 - x^2 - 31x + 35
Hence if (2x^3 - x^2 - 31x + 35) is divided by (2x - 7), the result is (x^2 + 3x - 5), the first polynomial of multiplication problem.
The polynomial (2x^3 - x^2 - 31x + 35) is called the dividend, (2x -7) is called the divisor, and (x^2 + 3x -5) is called the quotient. The first term of the dividend, 2x^3, comes from multiplying the first term of quotient, x^2, by the first term of the divisor, 2x. Thus to obtain the first term of quotient, x^2, we divide the first term of the dividend , 2x^3 , by the first term of the divisor, 2x. Multiplying the entire divisor (2x -7) by that first term of the quotient, x^2, we get 2x^3 - 7x^2. Subtracting 2x^3 - 7x^2 from the dividend,
(2x^3 - x^2 - 31x + 35) - (2x^3 - 7x^2) = 6x^2 - 31x + 35
The quantity 6x^2 - 31x + 35 is our new dividend. The first term, 6x^2, of the new dividend comes from multiplying the second term of the quotient, 3x, by the first term of the divisor, 2x. Thus to get the second term of the quotient, 3x, divide the first term of the new dividend, 6x^2, by the first term of the divisor, 2x. Multiplying the divisor (2x - 7) by the second term of the quotient, 3x, we get 6x^2 - 21x. Subtracting 6x^2 - 21x from the new dividend,
(6x^2 -31x +35) - (6x^2 - 21x) = -10x + 35
The quantity -10x + 35 is the new dividend. Dividing the first term of the new dividend (-10x) by the first term of the divisor, 2x, we get the third term of the quotient (-5). Multiplying the divisor (2x-7) by the third term of the quotient (-5), we get -10x + 35. Subtracting (-10x + 35) from the dividend (-10x + 35), We get zero.
Let us start the problem again an arrange it in a manner analogous to that of long division in arithmetic.

Hence (2x^3 - x^2 - 31x +35)/(2x - 7) = x^2 + 3x -5
DEFINITION The degree of a polynomial in a literal number is the greatest exponent of that literal number in the polynomial.
EXAMPLE x^5y - 7x^4y^2 - 2x^3y^3 + 9y^4 is a polynomial of degree 5 in x and degree 4 in y.
To divide two polynomials, we start by arranging the terms of the dividend according to the decreasing exponents of one of the literals, leaving spaces for the missing powers (including terms with zero coefficients for the missing terms). Arrange the terms of the divisor also according to the decreasing exponents of the same literal used in arranging the terms of the dividend. Divide the first term of the dividend by the first term of the divisor to get the first term of the quotient. Multiply the first term of the quotient by each term of the divisor and write the product under the like terms in the dividend. Subtract the product from the dividend to arrive at a new dividend.
To find the next term and all subsequent terms of the quotient, treat the new dividend as if it were the original dividend. Continue this procedure until you get zero or until the degree of the newly derived polynomial. with respect to the literal used in arranging the dividend, is at least one degree less than the degree of the divisor in that literal.
The last polynomial is called the remainder.
EXAMPLE Divide (6x^3 - 17x^2 + 16) by (3x - 4).
Solution Write the dividend as 6x^3 - 17x^2 + 0x + 16

EXAMPLE Divide (19x^2 - 10x^3 + x^5 - 14x + 6) by (x^2 + 1 -2x).
Solution Write the dividend as x^5 + 0x^4 - 10x^3 + 19x^2 - 14x + 6.
Write the divisor as x^2 -2x + 1
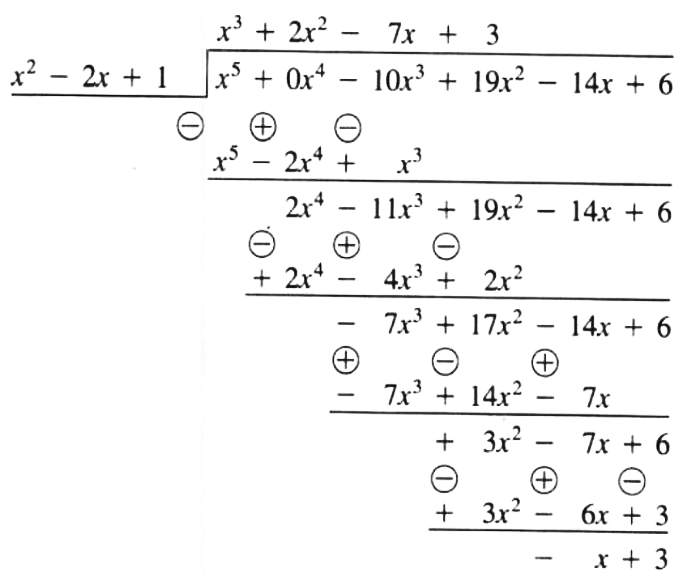
Hence (x^5 - 10x^3 + 19x^2 -14x + 6)/(x^2 - 2x + 1)
=x^3 + 2x^2 - 7x + 3 + (-x + 3)/(x^2 - 2x + 1)
=x^3 + 2x^2 - 7x + 3 - (x -3)/(x^2 - 2x + 1)
Note This form is similar to the form used in arithmetic when we write
20/7 = 2 + 6/7
EXAMPLE Divide (2x^4 - 3y^4 - 13x^2y^2 + 14xy^3) by (x^2 + 2xy - 3y^2)
Solution Write the dividend as 2x^4 + 0x^3y - 13x^2y^2 + 14xy^3 - 3y^4.

Hence (2x^4 - 13x^2y^2 + 14xy^3 - 3y^4)/(x^2 + 2xy -3y^2) = 2x^2 - 4xy + y^2