Linear systems in two variables

When an applied problem requires that more than one unknown quantity must be found, it is often helpful (or, in some cases, absolutely necessary) to write several equations in several variables, and then solve this resulting system of equations. At the college algebra level, we usually restrict the number of unknowns to two or three. After studying this chapter, it will become clear how the methods of solving systems can be extended to a larger number of unknowns. Graphing calculators and computers are able to solve systems of equations, eliminating the need for time-consuming computations. The methods of this chapter (especially those in can help the student appreciate the capabilities of today's electronic marvels.

Many applications of mathematics require the simultaneous solution of a large number of equations or inequalities having many variables. A group of equations that place restrictions on the same variables is called a system of equations. The solution set of a system of equations is the intersection of the solution sets of the individual equations. It is customary to write a system by listing its equations. For example, the system of equations  2x + y = 4 and x - y = 6 is written as

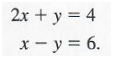
In general, a first-degree equation in n unknowns is any equation of the form

where a_1, a_2, . . . , a_n, and k are constants and x_1, x_2, . . . , x_n are variables. Such equations are also called linear equations. Generally, only systems of linear equations with two or three variables will be discussed in this book, although the methods used can be extended to systems with more variables.

The solution set of a linear equation in two variables is an infinite set of ordered pairs. Since the graph of such an equation is a straight line, there are three possibilities for the solution set of a system of two linear equations in two variables. An example of each possibility is shown in the figure below.

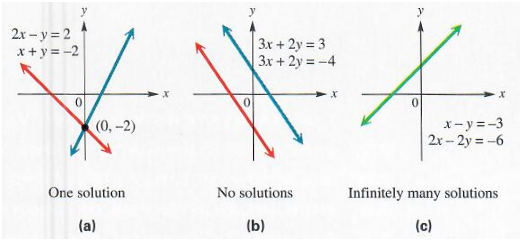
Possible graphs of a linear system with two equations and two variables

1. The graphs of the two equations intersect in a single point. The coordinates of this point give the solution of the system. This is the most common case. See Figure (a).
2. The graphs are distinct parallel lines. In this case, the system is said to be inconsistent. That is, there is no solution common to both equations. The solution set of the linear system is empty. See Figure b.
3. The graphs are the same line. In this case, the equations are said to be dependent, and any solution of one equation is also a solution of the other. Thus, there are infinitely many solutions. See Figure c.

Although the number of solutions of a linear system can often be seen from the graph of the equations of the system, it is usually difficult to determine an exact solution from the graph. A general algebraic method of finding the solution of a system of two linear equations, called the substitution method, is illustrated in the following example and used again later.