Literal Equations and Equations Involving Algebraic Fractions

7.6 Literal Equations

Some equations, called literal equations, involve more than one literal number. We can solve for one of the literals, called the variable, in terms of the other literals, Thus by assigning values for those literals. we obtain corresponding values for the variable.

To find the solution set of a literal equation, form an equivalent equation with all the terms that have the variable as a factor on one side of the equation and those terms that do not have the variable as a factor on the other side. Factor the variable from the terms that have the variable as a factor and then divide both sides of the equation by the coefficient of the variable.

Simplify the answer and check by substituting the value you obtained for the variable in the original equation.

EXAMPLE Solve the following equation for x: 2y-3x=8.

Solution 2y-3x=8

       -3x = 8-2y

       x=(8-2y)/-3 or x=(2y-8)/3

Hence the solution set is {(2y-8)/3}.

The check is left as an exercise.

EXAMPLE Solve the following equation for x:

  a(x-3)=2(1-x)

Solution a(x-3)=2(1-x)

       ax-3a = 2-2x

       ax+2x = 3a+2

       x(a+2) = 3a+2

If a+2 ≠ 0, that is a≠-2, we can divide both sides of the equation by (a+2) to get

       x=(3a+2)/(x+2)

Hence the solution set is 

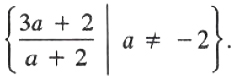
Note When a=-2, we have a false statement,

EXAMPLE Solve the following equation for x: 3ax+4 = 2x+6a.

Solution 3ax+4 = 2x+6a

=3ax-2x = 6a -4

=x(3x-2) = 6a-4

If (3a-2) ≠ 0, that is a ≠ 2/3, we can divide both sides of the equation by (3a-2) to get

       x=(3a-4)/(3a-2) = (2(3a-2))/(3a-2) = 2

Hence the solution set is 

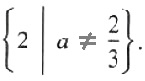
Note For any value for a ≠ 2/3 the value of x is 2, When a=2/3, the equation becomes an identity, that is, a statement that is true for all values of x.

Let’s see how our step by step math solver solves this and similar problems. Click on "Solve Similar" button to see more examples. 

EXAMPLE Solve the following equation for x and check:

  a(x+2) = a^2+4(x-2)

Solution  a(x+2) = a^2+4(x-2)

  ax+2a = a^2+4x-8

  ax-4x = a^2-8-2x

  x(a-4) = a^2-2a-8

  If (a-4) ≠ 0, that is, a ≠ 4, we can divide both sides of the equation by (a-4) to get 

  x=(a^2-2a-8)/(a-4)

  =((a-4)(a+2))/(a-4)

  =a+2

  To check, substitute a+2 for x in the original equation.

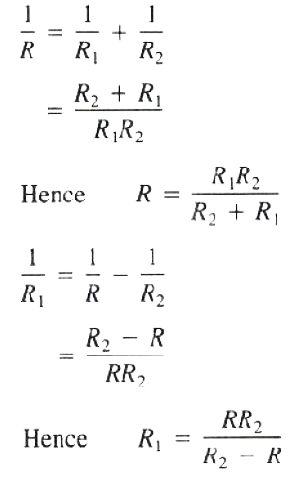
Formulas are rules expressed in symbols or literal numbers. They are widely used in many fields of study. Formulas may be considered special types of literal equations. Many problems require the solution of a formula for one of the letters involved.

EXAMPLE

Solution  

7.7 Equations Involving Algebraic Fractions

When an equation involves fractions, it can be put in a simpler form when both sides of the equation are multiplied by the LCD of all the fractions in the equation.

When an equation is multiplied by the LCD (which is a polynomial in the variable). the resulting equation may not be equivalent to the original equation. The ‘mulling equation may have a solution set with elements that do not satisfy the original equation. In all Such cases the elements in the solution set must be checked in the original equation.

The values of the variable that do not satisfy the original equation are called extraneous roots.

EXAMPLE Solve the equation 3/(4x)-1/(3x^2) = 5/(6x)

Solution Multiply both sides of the equation by 12x^2.

       3(3x)-4 = 5(2x)

       9x-4-10x

       x=-4

The solution set is {-4}.

EXAMPLE Solve the equation (2x)/(3x-4)-2 = 0

Solution Multiply both sides of the equation by (3x-4).

       2x-2(3x-4) = 0

       2x-6x+8 = 0

       -4x = -8

       x = 2

The solution set is {2}.

 The check is left as an exercise

EXAMPLE Solve the following equation and check:

       (x-3)/(x-4) - x/(2x+3) = x^2/(2x^2-5x-12)

Solution  (x-3)/(x-4) - x/(2x+3) = x^2/(2x^2-5x-12)

       (x-3)/(x-4) - x/(2x+3) = x^2/((2x+3)(x-4))

LCD = (x-4)(2x+3)

Multiplying both sides of the equation by (x-4)(2x+3) we get 

       (2x+3)(x-3)-x(x-4) = x^2

       (2x^2-3x-9)-(x^2-4x) = x^2

       2x^2-3x-9-x^2+4x = x^2

To check, substitute 9 for x in the original equation.

The solution set is {9}.

Let’s see how our step by step math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.   

EXAMPLE Solve the following equation

  (3x)/(6x^2-7x-3)-(x-2)/(2x^2-5x+3) = 3/(3x^2-2x-1)

Solution  (3x)/(6x^2-7x-3)-(x-2)/(2x^2-5x+3) = 3/(3x^2-2x-1)

  Multiplying both sides of the equation by (2x-3)(3x+1)(x-1), we get

  3x(x-1)-(x-2)(3x-1) = 3(3x-3)

  (3x^2-3x)-(3x^2-5x-2) = 6x-9

  3x^2-3x-3x^2+5x+2 = 6x-9

  -3x+5x-6x = -9-2

  -4x = -11

  x = 11/4

  The solution set is {11/4}

  The check is left as an exercise.

Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.  

EXAMPLE Solve the following equation and check:

  (x-3)/(3x-4)-(2x-5)/(6x-1) = (x-13)/(18x^2-27x+4)

Solution   (x-3)/(3x-4)-(2x-5)/(6x-1) = (x-13)/(18x^2-27x+4)

  Multiplying both sides of the equation by (6x-1)(3x-4), we obtain

  (6x-1)(x-3)-(3x-4)(2x-5) = x-13

  (6x^2-19x+3)-(6x^2-23x+20) = x-13

  6x^2-19x+13-6x^2+23x-20 = x-13

  3x = 4

  x = 4/3

  Substituting 4/3 for x in the original equation, we find that the denominator of the first fraction becomes zero. Since division by zero is not defined, the solution set of the equation is Φ