Quadratic Equation & Its Solutions

Completing the Square

The solutions to the quadratic equation x^2 = 5 are root(5) and -root(5), since (root(5))^2=5 and (-root(5))^2=5. In general, the following rule holds.

If x^2=a (a>0), then x=root(a) or x=-root(a). We can write x=+-root(a)

 

Examples

Solve the following quadratic equations.

1.     x^2=17

      x=+-root(17)    Keep in mind that the expression x=+-root(17)  represents the two equations, x=root(17) and x=-root(17)

2.     x^2=39

        x=+-root(39)

3.     (x+4)^2=7

        x+4=+-root(7)

        x=-4+-7

4.     2(x+9)^2=20/9

        (x+9)^2=10/9   Divide both sides by 2.

         x+9=+-root(10/9)

         x=-9+-root(10)/3

The example could also be written as follows to emphasize that there are two solutions.

2(x+9)^2=20/9 (x+9)^2=10/9 x+9=root(10/9)   or   x+9=-root(10/9) x=-9+root(10)/3     x=-9-root(10)/3

There is no real number whose square is negative. So, to solve equations such as x^2 = -4 and (x - 3)^2 = -10, numbers called complex numbers are needed. These numbers will be discussed in the next course in algebra.

           What should be added to x^2 - 8x to get a perfect square trinomial? The answer is 16.

x^2-8x+16=(x-4)^2      ((1/2(-8)=-4  and (-4)^2=16)

This procedure is called completing the square and was discussed in another Section. We can use this procedure to solve quadratic equations. For example, to solve the equation x^2 - 6x + 4 = 0, we might try factoring, as in previous Section, but x^2 - 6x + 4 will not factor. The technique of solving by completing the square is explained in the following examples. The coefficient of x^2, the leading coefficient, must be 1 for the technique to work.

Examples

1.   x^2-6x+4=0

     x^2-6x=-4                 -4 is added to both sides of the equation.

     x^2-6x+9=-4+9         9 is added to both sides of the equation. The left side is now a perfect square trinomial.

                                                  1/2(-6)=-3 and (-3)^2=9

(x-3)^2=5                       Simplify. x-3=+-root(5)                   Find square roots. x=3+-root(5)                      Solve for x.

2.    x^2 + 5x = 7                                 Complete the square on the left.

      x^2 + 5x+25/4 = 7+25/4            1/2*5=5/2 and (5/2)^2=25/4

(x+5/2)^2=53/4                         Simplify x+5/2=+-root(53/4)                     Find square roots. x=-5/2+-root(53/4)                  Solve for x. x=-5/2+-root(53)/2                  Special property of square roots

                                                          root(a/b)=root(a)/root(b) for a>0 and b>0

x=(-5+-root(53))/2 Simplify

 

3.    6x^2 + 12x - 9 = 0

       6x^2 + 12x = 9                            Add 9 to both sides of the equation.

      (6x^2)/6+(12x)/6=9/6                       Divide each term by 6 so that the leading coefficient will be 1.

      x^2+2x=3/2                               The leading coefficient is 1.

      x^2+2x+1=3/2+1                  Complete the square, 1/2*2=1 and 1^2=1

     (x+1)^2=5/2                              Simplify.

     x+1=+-root(5/2)                          Find square roots.

     x=-1+-root(5/2)                           Solve for x.

     x=-1+-root(5)/root(2)*root(2)/root(2)               Rationalize the denominator.

     x=-1+-root(10)/2                         Simplify.

or  x=(-2+-root(10))/2

 

4.   2x^2 + 5x - 8 = 0

     2x^2+5x=8                               Add 8 to both sides of the equation.

    (2x^2)/2+(5x)/2=8/2                         Divide each term by 2 so that the leading coefficient will be 1.

    x^2+5/2x=4                               Simplify.

    x^2+5/2x+25/16=4+25/16          Complete the square, 1/2*5/2=5/4 and (5/4)^2=25/16

    (x+5/4)^2=89/16                        Simplify.

    x+5/4=+-root(89/16)                         Find the square roots.

    x=-5/4+-root(89)/4                       Solve for x, also root(89/16)=root(89)/root(16)=root(89)/4

x=(-5+-root(89))/4                                 Simplify.

5.   x^2 + 8x = -4

     x^2 + 8x+16 = -4+16          Complete the square.

    (x+4)^2=12                           Simplify. 

     x+4=+-root(12)                           Find square roots.

     x=-4+-root(12)                         Solve for x.

     x=-4+-2root(3)                        root(12)=root(4)*root(3)= 2root(3)  by special property

root(ab)=root(a)*root(b) for a>0 and b>0.

The Quadratic Formula

The quadratic formula is a general method for solving second degree equations of the form ax^2 + bx + c = 0 where a, b, and c can be any real numbers. The quadratic formula is a very old formula; it was known to Babylonian mathematicians around 2000 B.C. However, Babylonian, and later, Greek mathematicians always discarded negative solutions of quadratic equations because they felt that these solutions had no physical meaning. Greek mathematicians always tried to interpret their algebraic problems from a geometrical viewpoint and hence the development of the geometric method of "completing the square."

Consider the following equation: x^2 + 6x = 7. A geometric figure is constructed having areas x^2, 3x and 3x. Note that, in order

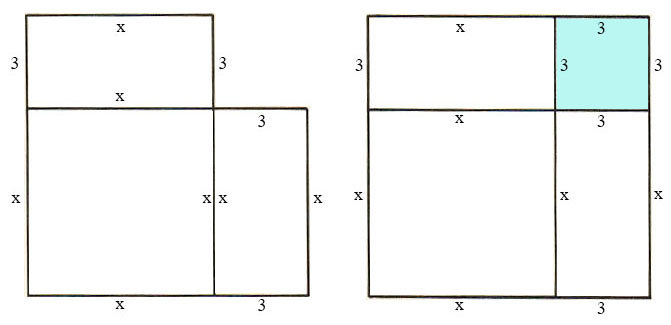
to make the figure a square, a 3 by 3 section (area = 9) must be added. Thus, 9 must be added to both sides of the equation to restore equality. Thus,

         x^2+6x=7

and  x^2+6x+9=7+9

       x^2+6x+9=16

So, the square with side x + 3 now has an area of 16 square units. Therefore, the sides must be of length 4, which means x + 3 = 4.

Hence, x = 1.

Note that actually the solution set of the original equation is {1, -7}, since (-7)^2 + 6(- 7)= 49 - 42=7. Thus the Greek mathematicians "lost" the negative solution because of their strictly geometric interpretation of quadratic equations. There were, therefore, many quadratic equations that the Greek mathematicians could not solve because both solutions were negative numbers or complex numbers. Negative solutions to equations were almost completely ignored until the early 1500s during the Renaissance.

Development of the Quadratic Formula

Now we are interested in developing a formula that will be useful in solving quadratic equations of any form. This formula will always work, but the student should not forget the factoring and completing the square techniques because they can be easier to apply than the formula.
         The general quadratic equation is

ax^2+bx+c=0, a!=0

We want to solve the general quadratic equation for x in terms of the coefficients a, b, and c. The technique is to complete the square, treating a, b, and c as constants.

ax^2+bx+c=0, a>0

ax^2+bx=-c                                             Add -c to both sides.

(ax^2)/a+(bx)/a=-c/a                                        Divide each term by a.

x^2+b/ax=-c/a                                           Simplify: (bx)/a=b/ax

x^2+b/ax+(b/(2a))^2=(b/(2a))^2+(-c)/a           Complete the square, 1/2(b/a)=b/(2a)

(x+b/(2a))^2=b^2/(4a^2)+(-c)/a                           Simplify

(x+b/(2a))^2=b^2/(4a^2)+(-c*4a)/(a*4a)                 Common denominator is 4a^2

(x+b/(2a))^2=(b^2-4ac)/(4a^2)                               Simplify

x+b/(2a)=+-root((b^2-4ac)/(4a^2))                                 Find the square roots.

x+b/(2a)=+-root(b^2-4ac)/+-root(4a^2)                                   Use the relationship root(a/b)=root(a)/root(b)             if a, b>0

x+b/(2a)=+-root(b^2-4ac)/(2a)                                 Simplify

x=(-b)/(2a)+-root(b^2-4ac)/(2a)                               Solve for x.

x=(-b+-root(b^2-4ac))/(2a)                                     THE QUADRATIC FORMULA

      Special Note: The expression b^2 - 4ac is called the discriminant. If b^2 - 4ac < 0, then there are no real number solutions. A discussion of negative discriminants is given in later courses in algebra.

      Now the solutions to quadratic equations can be found by going directly to the formula.

Examples

Solve the following quadratic equations using the Quadratic Formula.

1.  2x^2+x-2=0

     a=2, b=1 and c=-2

x=(-1+-root(1^2-4(2)(-2)))/(2*2)=(-1+-root(1+16))/4=(-1+-root(17))/4

This is how our quadratic equation step by spte solver solves the problem above. You can see similar problems solved by clicking on 'Solve similar' button.

2.   3x^2-5x+1=0

     a=3, b=-5 and c=1

x=(-(-5)+-root((-5)^2-4(3)(1)))/(2*3)=(5+-root(25-12))/6=(5+-root(13))/6

3.   1/6x^2-x+1/2=0

     6*1/6x^2-6*x+6*1/2=6*0     Multiply each term by 6, the least common denominator.

     x^2-6x+3=0

     a=1, b=-6 and c=3

x=(-(-6)+-root((-6)^2-4(1)(3)))/(2*1)=(6+-root(36-12))/2

= (6+-root(24))/2=(6+-2root(6))/2=3+-root(6)

Note:

(6+-root(4)*root(6))/2=(6+-2root(6))/2=6/2+-(2root(6))/2=3+-root(6)

4.   -5x^2+3x=-2

     -5x^2+3x+2=0      One side must be zero

     a=-5, b=3 and c=2

x=(-3+-root(3^2-4(-5)(2)))/(2(-5))=(-3+-root(9+40))/-10=(-3+-root(49))/-10=(-3+-7)/-10

    x=(-3+7)/-10=4/-10=2/-5   or   x=(-3-7)/-10=-10/-10=1

Example 4 could have been solved by factoring:

   -5x^2+3x+2=0

   5x^2-3x-2=0        Multiply both sides of the equation by -1.

  (5x+2)(x-1)=0

   5x+2=0     or    x-1=0

   5x=-2              x=1

   x=2/-5

Such equations should be solved by factoring because factoring is generally easier than applying the quadratic formula. However, if you do not “see” the factors readily, the quadratic formula will give the solutions, as this
example illustrates.

This is how our factorization calculator solves the problem above. You can see similar problems solved by clicking on 'Solve similar' button.

 

Article Summary

 

If a and b are positive real numbers, then             1.   root(ab)=root(a)root(b) and      2.   root(a/b)=root(a)/root(b)

A radical is considered to be in simplest form when the radicand has no square number factor.

To simplify the sum or difference of radicals, proceed by combining like radicals just as in combining like terms.

To rationalize the denominator of a fraction, multiply the numerator and denominator by a number that will give a denominator that is a rational number.

If x^2=a ((a>0)), then x=root(a) or x=-root(a). We can write x=+-root(a)

To complete the square of a binomial, add a square constant so that the resulting trinomial is a perfect square trinomial.

The general quadratic equation is:

ax^2+bx+c=0    a!=0

The QUADRATIC FORMULA is:

x=(-b+-root(b^2-4ac))/(2a)