Solutions by graphing, substitution, and addition

9.1 Solutions by Graphing

  Visualize two straight lines on the same graph. What two lines did you see‘? No matter what specific lines you envisioned, there are only three basic positions for the lines relative to each other. What do you think they are’? Stop to think about your lines and those of the other people in class before you read further.

  Do the lines y = -x + 4 and y = 2x + 1 intersect (cross each other)? If so, where do they intersect? If not, why not? We can answer these questions by graphing both equations as in Figure 9.1.

  

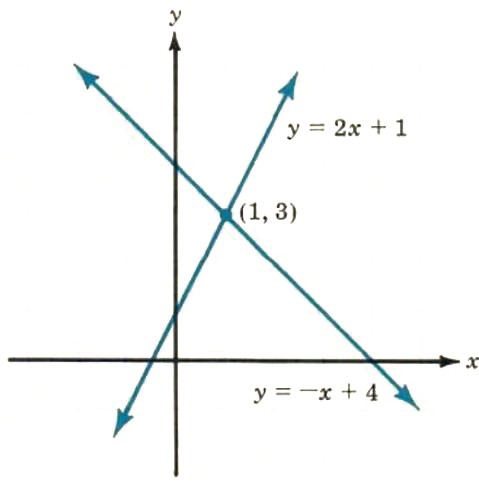
  Figure 9.1

  The lines appear to intersect at the point (1, 3), or where x = 1 and y = 3. This intersection can be checked by substituting x = 1 and y = 3 into both equations:

  y=2x+1

  3=2*1+1

  3=3

  y=-x+4

  3=-1+4

  3=3

  The lines do intersect at (1, 3).

  

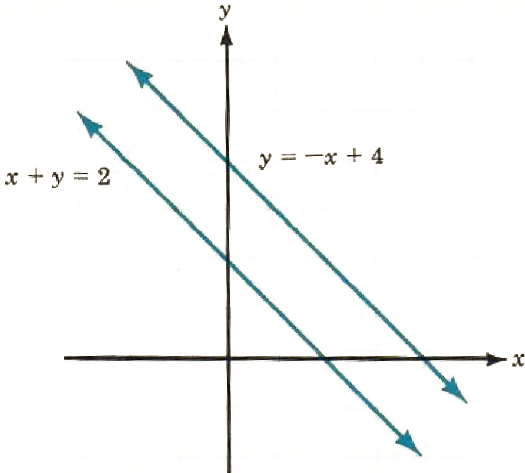
  Figure 9.2

  Do the lines y = -x + 4 and x + y = 2 intersect? If so, where do they intersect? If not, why not? The answers are in the graphs in Figure 9.2.

  The lines do not intersect because they are parallel. In this case, we could have anticipated the result by writing both equations in the intercept form and noted that both lines have the same slope, -1:

  y=-x+2  m=-1

  y=-x+4  m=-1

  Do the lines y=-x+4 and 2y + 2x = 8 intersect? If so, where do they intersect? If not, why not? The graphs of both lines are shown in Figure 9.3. Why is there just one line?

  The reason there is just one Line is that both equations represent the

  

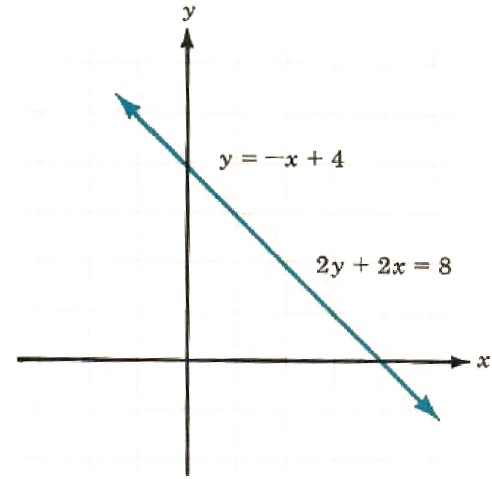
  Figure 9.3

  same line. The lines not only intersect; they are the same line. That is, they coincide. Any point that satisfies one equation will also satisfy the other This can be seen easily by putting both equations in the slope-intercept form :

  y=-x+4  2y+2x=8

  2y=-2x+8

  (2y)/2=(-2x+8)/2

  y=-x+4

  Both equations are identical when written in the same form.

  These three examples constitute all three possible situations involving the graphs of two linear equations. When two linear equations are considered together, they are called a system of linear equations, or a set of simultaneous equations. The term simultaneous is frequently used to emphasize the idea that the solution of a system is the point that satisfies both equations at the same time, or simultaneously.

  If a system has a unique solution (one point of intersection), the system is consistent. If a system has no solution (the lines are parallel with no point of intersection), the system is inconsistent. If a system has an infinite number of solutions (the lines coincide), the system is dependent.

  The following table summarizes the basic ideas and terminology.

System	Graph	Intersection	Terms
y=-x+4 y=2x+1		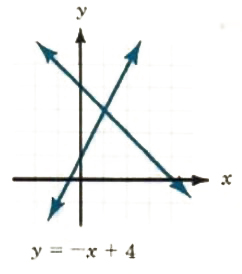one point: (1, 3)	consistent
y=-x+4 x+y=2		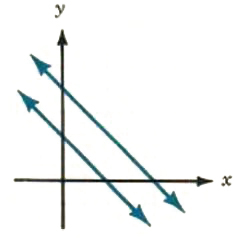no points; lines are parallel	inconsistent
y=-x+4 2x+2y=8		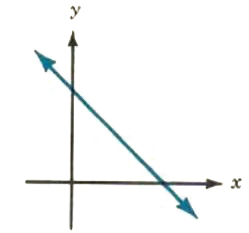infinite number of points; lines are the same (&hey coincide)	dependent

Examples

  Determine graphically whether the fallowing systems are (a) consistent, (b) inconsistent, or (c) dependent. If the system is consistent, find the point of intersection.

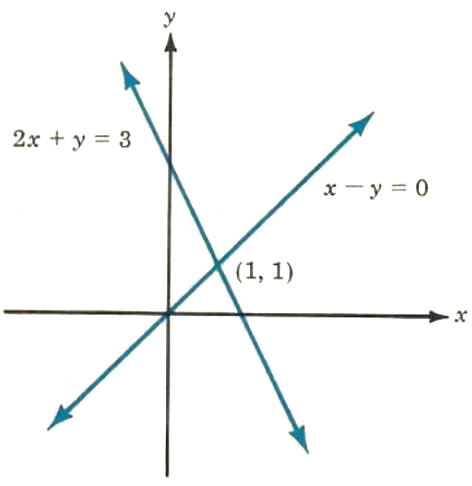
  1. x-y=0 2x+y=3

  The system is consistent. The point of intersection is (1, 1).

  Checking: x=1, y=1

  1-1=0

  2.1+1=3

    

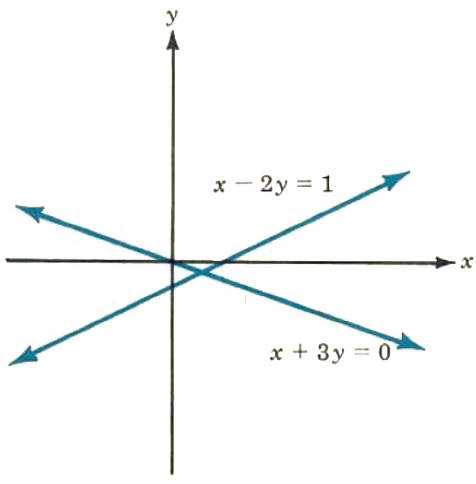
  2. x-2y=1,x+3y=0

  The system is consistent, but the point of intersection can only be estimated. This example points out the main weakness in solving a system graphically. In such cases, any reasonable estimate will be acceptable. For example, if you estimated (1/2,-1/4). or (3/4,-1/3) some such point, your answer is acceptable. The actual point of intersection is (3/5,-1/5). We will be able to locate this point precisely using the techniques of the next section.

  

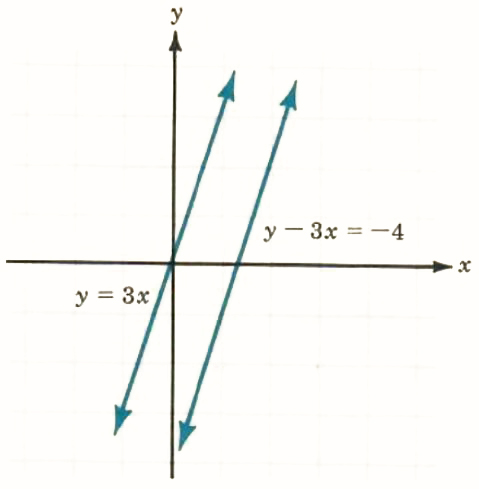
  3. y=3x,y-3x=-4

  The system is inconsistent. The lines are parallel with the same slope, 3, and there are no points of intersection.

  

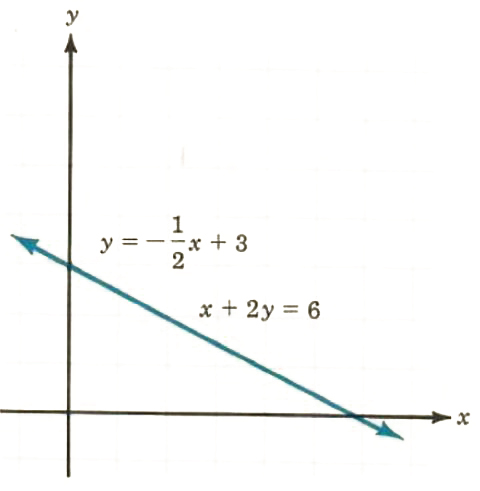
  4. x+2y=6,y=-(1/2x)+3

  The system is dependent. All points that lie on one line also lie on the other line. For example, (4, 1) is a point on the line x + 2y = 6 since 4 + 2(1) = 6. The point (4, 1) is also on the line y = -(1/2)x+ 3 since 1 = -(1/2)(4) + 3.

  

9.2  Solutions by Substitution

  Solving a system of linear equations graphically can be time-consuming and does not always yield accurate results. When the system has one equation that can easily be solved for one of the variables, the algebraic technique of substitution is convenient. We simply substitute an expression for a variable from one equation into the other. For example, consider the system

  y=-2x+5,x+2y=1

  How would you substitute? The first equation is already solved for y. Would you put -2x + 55 for y in the second equation? Try this and see what happens.

  x+2(-2x+5)=1

  We now have one equation in only one variable, x. We have reduced the problem of solving two equations in two variables to solving one equation in one van'able. Solve the equation for x. Then find the corresponding y-value from either of the two original equations.

  x+2(-2x+5)=1

  x-4x+10=1

  -3x=-9

  x=3

  Substituting x=3 into y=-2x+5 gives

  y=-2*3+5

  =-6+5=-1

   The solution is x = 3, y = -1 or the point (3, -1).
Substitution is not the only algebraic technique for solving a system of linear equations. It does work in all cases but is generally used only when one equation is easily solved for one variable.

  Solve the system using the technique of substitution. 

  3x+y=1,6x+2y=3

  for  3x+y=1

  y=-3x+1

  Substituting   6x+2y=3

  6x+2(-3x+1)=3

  6x-6x+2=3

  This last equation, 2 = 3, is never true; and this tells us that the system is inconsistent. The lines are parallel and there is no point of inter section.

  Solve the system using the technique of substitution.

  x-2y=1,3x-6y=3

  for  x-2y=1

  x=2y+1

  Substituting   3x-6y=3

  3(2y+1)-6y=3

  6y+3-6y=3

  3=3

  This last equation, 3=3, is always true; and this tells us that the system is dependent. The two lines are the same and there are an infinite number of points of intersection.

Examples

  Solve the following systems of linear equations using the technique of substitution.

  1. y=5/6x+1,2x+6y=7

  y=5/6x+1 is already solved for y.

  Substituting   

  2x+6y=7

  2x+6(5/6x+1)=7

  2x+5x+6=7

  7x=1

  x=1/7  y=5/6*1/7+1=5/42+42/42=47/42

  The solution is (1/7,47/42) or x=1/7 and y=47/42.

  2. x+3y=0,-4x+2y=7

  Solving for x

  x+3y=0

  x=-3y

  Substituting,

  -4x+2y=7

  -4(-3y)+2y=7

  12y+2y=7

  14y=7

  y=1/2  x=-3(1/2)=-(3/2)

  The solution is (-3/2,1/2), or x=-(3/2) and y=1/2.

Let’s see how our linear equation solver solves this and similar problems. Click on "Solve Similar" button to see more examples. 

  3. x=-5,y=2x+9

  x=-5 is already solved for x. The equation represents a vertical line. Substituting, 

  y=2x+9

  y=2(-5)+9=-10+9=-1

  The solution is x=-5 and y=-1 or (-5,-1).

9.3  Solutions by Addition

  The system x+y=4,x-y=6 can be solved using the algebraic technique of substitution discussed in Section 9.2. The technique of addition is also convenient and, in this case, probably easier than substitution. Put both equations in the standard form Ax + By = C and set up one under the other so that like terms are aligned. Then add like term.

  

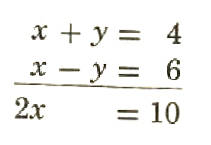
  Since +y and -y have opposite coefficients, the y-terms are eliminated, and the resulting equation, 2x=10, has only one variable. Just as with the technique of substitution, the solution of the system is reduced to solving
one equation in one variable.

  

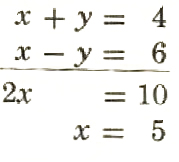
5+y=4 y=-1

  The solution is x=5,y=-1.

  If the two coefficients of one variable in the system are not opposites, then we multiply each equation by some nonzero constant so that either the two x-coefficients are opposites or the two y-coefficients are opposites For example, consider the system

  4x-3y=1,3x-2y=4

  Multiplying each term of the first equation by 2 and each term of the second equation by -3 will result in the y-coefficients being opposites. Or multiplying the terms of the first equation by 3 and the second equation by -4 will give opposite coefficients for the x-terms. Both cases yield the same solution and are illustrated below. The number used to multiply the terms of each equation is in brackets.

  Method 1. Eliminate y-terms

    

  4x-3y=1

  4*10-3y=1

  40-3y=1

  -3y=-39

  y=13

  The solution is x=10, y=13.

Method 2.  Eliminate x-terms

  

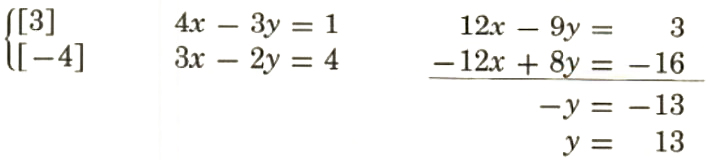
  4x-3y=1

  4x-3*13=1

  4x-39=1

  4x=40

  x=10

  As illustrated in Method 1 and Method 2, eliminating either the y-terms or the x-terms yields the same results. What if both the x- and y-terms are eliminated? In this situation, the system is either inconsistent or dependent. Just as with the technique of substitution, the resulting equation involving only constants tells which case is under consideration.

  For the system

  2x-y=6,4x-2y=1

  multiplying the terms in the first equation by -2 and then adding gives

  

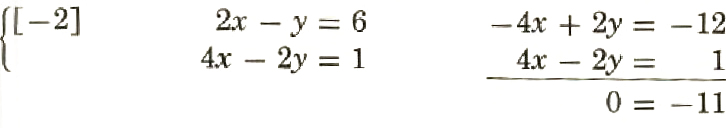
  Since the equation 0=-11 is not true, the system is inconsistent. There is no solution.

  For the system

  2x-2y=1,3x-3y=3/2

  multiplying the terms in the first equation by 3 and the terms in the second equation by -2 and then adding gives

  

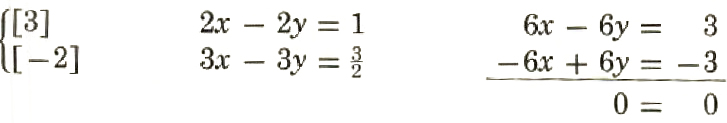
  Since the equation 0 = 0 is always true, the system is dependent.
  In solving a system by addition, find the constant for multiplying the terms of each equation by trying to get coefficients of like terms to be opposites. There are many possible choices. One approach is to find the least common multiple of the two coefficients already there, and then multiply so that one coefficient will be the LCM and the other coefficient, its opposite.

  Thus, for the system

  4x-3y=1,3x-2y=4

  in Method 1 the coefficients for the y-terms ended up being -6 and +6. The LCM for 3 and 2 is 6. In Method 2, the coefficients for the x-terms ended up being +12 and -12. The LCM for 4 and 3 is 12.

Examples

  Solve the following systems of equations using the technique of addition.

  1.  

  The solution is x=1,y=1.

  (In this example, multiplying the terms of the first equation by -2 and eliminating the x-terms would have given the same results.)

  2. 5x+3y=-3,2x-7y=7

  

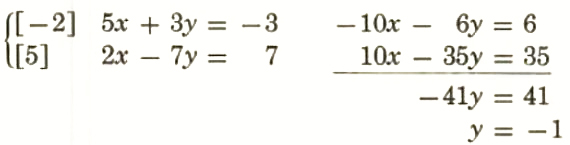
  5x+3(-1)=-3

  5x-3=-3

  5x=0

  x=0

  The solution is x=0, y=-1.

Let’s see how our linear equation solver solves this and similar problems. Click on "Solve Similar" button to see more examples. 

  3 x+y=5,x+y=6

  

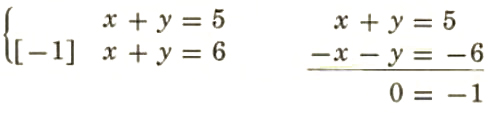
  There is no solution. The system is inconsistent.

  4.

  

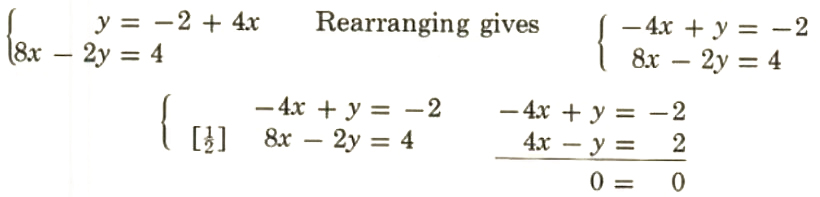
  The system is dependent.

  5. Using the formula y = mx + b, find the equation of the line determined by the two points (3, 5) and (-6, 2).
Solution:  Write two equations in m and b by substituting the coordinates of the points for x and y.

  

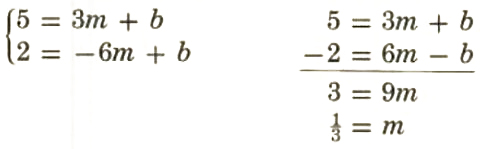
  5=3*1/3+b

  5=1+b

  4=b

  The equation is y=1/3x+4.

9.4  Applications

  We have solved word problems in several previous sections, but those problems were all solved with one equation in one variable. Many of these same problems can be solved using two equations in two variables. Here is Example 2 just as solved in Section 7.3.

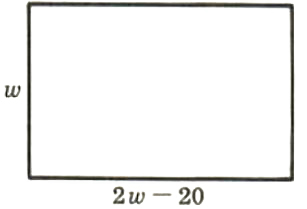
Example  A rectangle with perimeter 140 meters has a length that is 20 meters less than twice the width. Find the dimensions of the rectangle.

Solution:  Draw a diagram and use the formula P = 2l+ 2w.

  Let  w= width

  2w-20= length

  2(w)+2(2w-20)=10

  2w+4w-40=140

  6w=180

  w=30 meters

  2w-20=40 meters

  

  How would you solve this same problem using two equations in two variables? If you are going to use two variables, each variable must represent a different quantity. What are the two quantities in this case?

  Let  x=width

      y=length

  

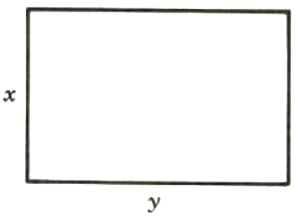
  Now we need two equations. Knowing the perimeter gives one relationship between the width and length. What is the other relationship? The phrase “a length that is 20 meters less than twice the width” gives the necessary information.

  The two equations are

  

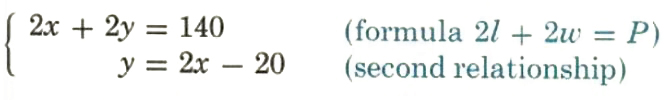
  Solving by substitution gives

  2x+2(2x-20)=140  (the same equation arrived at using one variable)

  2x+4x-40=140

  6x=180

  x=30 meters

  y=2(30)-20=40 meters

  Obviously, we have the same solution as before. The basic difference is that the thinking is easier. The technique can also be expanded to handle more difficult problems later on.

  Consider the following solution to Example 2 of Section 7.4.

Example  A woman has $7000. She decides to separate her funds into two investments. One yields an interest of 6% and the other, 10%. If she wants an annual income from the investments to be $580, how should she split the money?

Solution:

  Letx= amount invested at 6%

    y= amount invested at 10%

  x+y=7000  (total invested is $7000.)

  0.06x+0.10y=580  (total interest is $580.)

  

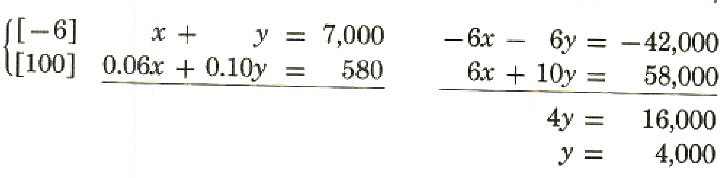
  x+4000=700

  x=3000

  x= $3000 invested at 6%

  y= $4000 invested 10%

Examples  1. How many ounces each of a 10% salt solution and a 15% salt solution must be used to produce 50 ounces of a 12% salt solution?

Solution:

  Let x= amount of 10% solution

     y= amount of 15% solution

  amount of solution ⋅ present of salt = amount of salt

10% solution	x	0.10	0.10x
15% solution	y	0.05	0.15y
12% solution	50	0.12	0.12(50)

 

  

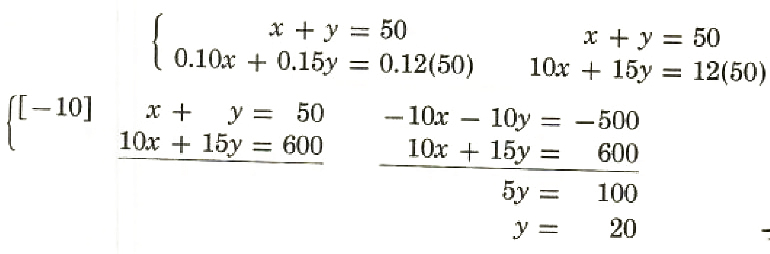
  x+20=50

  x=30

  x=30 ounces of 10% solution

  y=20 ounces of 15% solution

  2. One number is three less than twice the other, and their product is 83 more than their sum. Find the numbers.

Solution:

  Let x= one number

     y= second number

  y=2x-3,xy=x+y+83

  Solve by substitution. The elimination method does not work here because a product is involved. The resulting equation is quadratic.

  x(2x-3)=x+(2x-3)+83

  2x^2-3x=3x+80

  2x^2-6x-80=0

  x^2-3x-40=0

  (x-8)(x+5)=0

    x-8=0  or  x+5=0

    x=8          x=-5

    y=2*8-3    y=2(-5)-3

    y=13      y=-13

  3. A small plane flew 300 miles in 2 hours. Then on the return trip, flying against the wind, it traveled only 200 miles in 2 hours. What were the wind velocity and the speed of the plane?

Solution:

  Let s= speed of plane

     v= wind velocity

    rate ⋅ time = distance

  

with the wind	s+v	2	2(s+v)
against the wind	s-v	2	2(s-v)

  

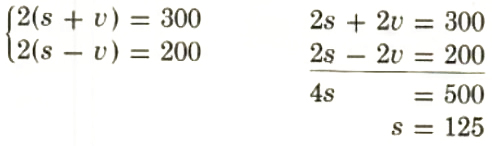
  2(125+v)=300

  125+v=150

  v=25

  s=125 mph

  v=25 mph

APPENDIX I:  Negative Exponents and Scientific Notation

  In Working with exponents, we have developed the following properties for whole number exponents where a is a nonzero real number and m and n are Whole numbers.

  1. a^m*a^n=a^(m+n)

  2. a^0=1

  3a. (a^n)/(a^m)=a^(n-m) if n>=m

      b. (a^n)/(a^m)=1/a^(n-m) if m>n

  4. (ab)^n=a^(n)b^(n)

  5. (a/b)^n=(a^n)/(b^n)

  6. (a^m)^n=a^(mn)

  These same properties are valid if the exponents are negative integers. To understand the meaning of negative exponents, consider the following discussion.

  Investigate the following patterns and try to anticipate the results.

  2^3=8  3^3=27

  2^2=4  3^2=9

  2^1=2  3^1=3

  2^0=1  3^0=1

  2^-1=?  3^-1=?

  2^-2=?  3^-2=?

  The pattern is that 2^-1=1/2 and 2^-2=1/4. Also, 3^-1=1/3 and 3^-2=1/9. 

  For another approach to the same idea, we know that

  (3^3)/(3^5)=(3*3*3)/(3*3*3*3*3)=1/3^2=1/9 or (3^3)/(3^5)=1/(3^(5-3))=1/(3^2)=1/9

  using Property 3b for exponents. If we apply Property 3a and allow negative exponents, we get

  (3^3)/(3^5)=3^(3-5)=3^-2

  So,

  3^-2=1/(3^2)=1/9seems quite reasonable.

  We now have Property 7 for integer exponents

  Property 7 for Exponents

  If a is a nonzero real number and n is an integer, then 

  a^-n=1/(a^n)

  The following examples show how expressions can be simplified using all seven properties applied to negative exponents.

Examples  Simplify the following expressions.

  1. 2^-3=1/(2^3)=1/8

  2. x^-3=1/(x^3)

  3. 5^-1=1/5

  4. (x^-2)/(x^-7)=x^(-2-(-7))=x^(-2+7)=x^5

  5. (x^6)/(x^(-1))=x^(6-(-1))=x^7

  6. (x^-6)/(x^-1)=x^(-6-(-1))=x^(-6+1)=x^-5 or 1/(x^5)

  x^-5 and 1/(x^5)are both acceptable answers. Both are correct. The choice generally depends on further uses of the expression.

  7. (x^7*x^-3)/(x^-2)=(x^(7-3))/(x^(-2))=(x^4)/(x^-2)=x^(4-(-2))=x^6

  8. (x^-2)^-3=x^(-2(-3))=x^6

  9. (2y^-1)^-2=2^-2y^2=1/4y

  10 (10^-3*10^4)/(10^6*10)=(10^(-3+4))/(10^(6+1))=(10^1)/(10^7)=10^(1-7)=10^(-6)

  One of the most fundamental uses of exponents on an elementary level occurs in the scientific notation used in physics, chemistry, and other scientific and technological fields. This notation is particularly convenient because it simplifies calculations with very large and very small numbers.

  For example, you might Want to multiply the distance to the sun from the earth by the distance to the moon from the earth. The calculations in scientific notation would look like this:

  93,000,000× 250,000  (In scientific notation, a cross, ×, is used to indicate multiplication.) 

    =9.3×10^7×2.5×10^5

    =9.3×2.5×10^7×10^5

    =23.25×10^12

    =2.325×10^13

  In scientific notation, all decimal numbers are written as the product of a number between 1 and 10 and a power of 10. This notation is quite common in the hand-held calculators available to most students.

  56,000=5.6×10^4  (Note: 1<5.6<10)

  0.00056=5.6×10^-4

  The exponent tells how many places the decimal point is to be moved and in what direction. In 5.6 × 10^4, the decimal point should got four places to the right (positive direction). 5.6 × 10^4 = 5.6000=56,000. In 5.6×10^-4 , the decimal point should go four places to the left (negative direction). 5.6×10^-4=0005.6=0.00056.

  For fun, see if you can write the number of miles in a light year in scientific notation. A light year is the distance that light travels in one year. Light travels at a rate of 186,000 miles per second.

Examples  Write the following decimals in scientific notation.

  1. 940,000=9.4×10^5

  2. 0.00381=3.81×10^-3

  3. 8,720,000=8.72×10^6

  4. 3000,000×700=3×10^5×7×10^2

        =21×10^7=2.1×10^1×10^7=2.1×10^8

  5.  

       

APPENDIX ll:  Graphing Linear Inequalities

  The points that satisfy the equation y = -2x + 3 lie on a straight line. For each value of x, the corresponding y-value is -2x + 3. Each point on the line is of the form (x, -2x + 3). For example, if x = 2, then y = -2*2 + 3 = -4+3 = -1; so the point (2, -1) or (2, -2*2 + 3) is on the line. (See Figure II.1.)

    

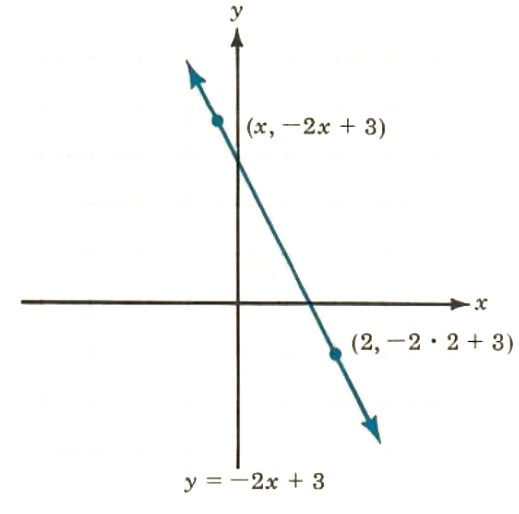
  Figure II.1

  Where are the points in the plane where y < -2x + 3? Where are the points where y > -2x + 3? We know the points where y = -2x + 3 are on a line. Pick two points, one above the line and one below the line. Any two points will do, just so they are obviously on opposite sides of the line. For example, the points (2, 1) and (2, -4) are shown in Figure II.2.

  

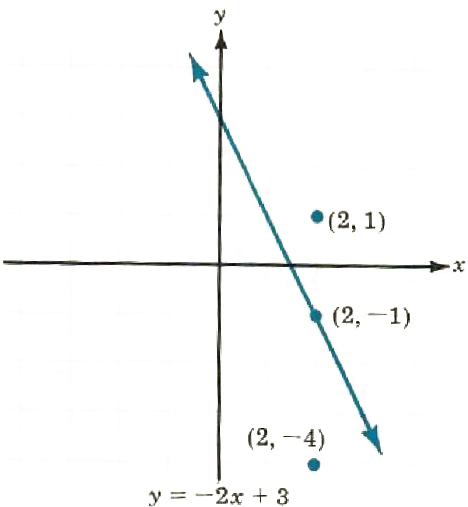
  Figure II.2

  The point (2, -4) is below the point (2,-1) since -4<-1. Therefore, at least for x = 2,-4 < -2x + 3.
What about other points below the line? Will the y-value be less than -2x + 3? Choose another point below the line, say (0,1/2). For x = 0, -2x + 3 = -2(0) + 3 = 3. Thus, for the point (0,1/2) below the line, 1/2<-2x + 3. In fact, this will always happen for points below the line. The set of points that satisfy the inequality y < -2x + 3 are below the line y=-2x+3. (See Figure II.3.)

  

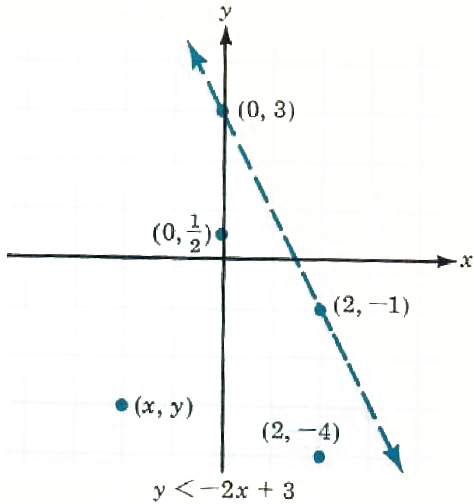
  Figure II.3

  (The line y = -2x + 3 is dotted to show that the points on the line are not included in the graph.)

  Now it should be clear that the points where y > -2x + 3 are above the line y = -2x + 3. The point (2, 1) above the line satisfies the relation ship 1 > -2x + 3. y > -2(2) + 3 (See Figure II.4.)

  

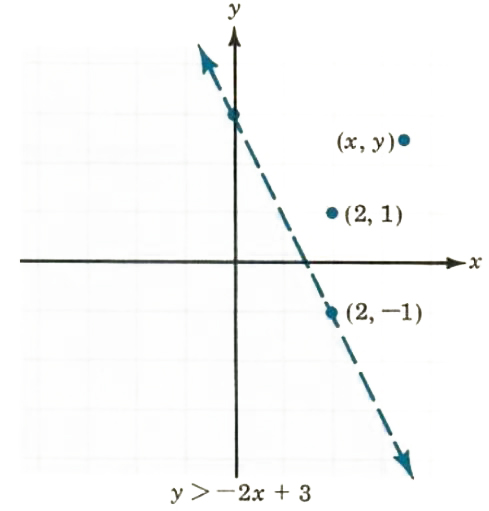
  Figure II.4

Examples  1. Graph the points that satisfy the linear inequality 2x + 3y < 6.
Solve for y,

  2x + 3y < 6

  3y<-2x+6

  y<(-2x+6)/3

  y<-(2/3)x+2 The points are below the line y=-(2/3)x+2.

  

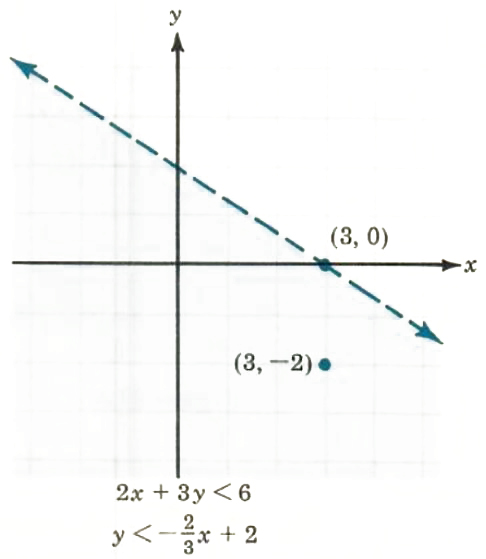
  Checking one points: For (3,-2),-2<-(2/3)(3)+2 or -2<0. Or 2(3)+3(-2)=6-6 6-6=0.

  2. Graph the points that satisfy the linear inequality 5x-y<=4.

  Solving for y,

  5x-y<=4

  5x-4<=y

  or y>=5x-4 The points are above and on the line y=5x-4.

    

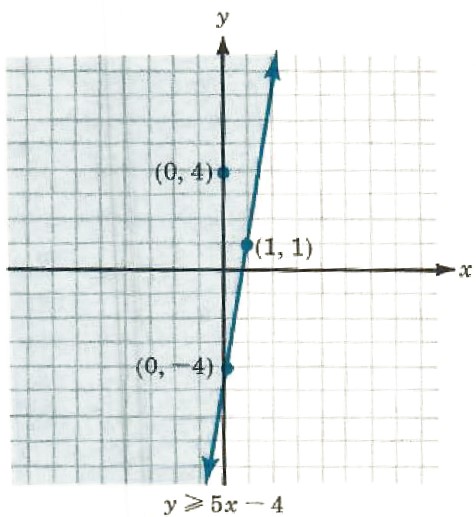
  Checking one points: For (0,4),4>5*0-4 or 4>=-4. Or, 5*0-4=-4 -4<=4.

  To see that checking one point is sufficient, try a point below the line, say (1,-2). Is -2>=5*1-4? Since 5*1-4=1 and   the points that satisfy the inequality y>=5x-4 or 5x-y<=4 are above and on the Line.

  3. Graph the points that satisfy both inequalities x<=2 and y>=-x+1. For x<=2, the points are to the left of and on the line x=2. For y>=-x+1, the points are above and on the line y=-x+1. The points that satisfy both conditions are shown in the shaded portion and solid lines of the graph.

  (x<=2) and (y>=-x+1)

  

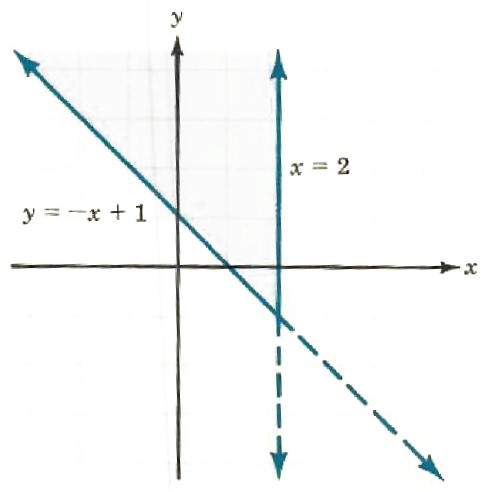
Let’s see how our math solver solves this and similar problems. Click on "Solve Similar" button to see more examples.